Y intercept of parabola

First, identify the slope and a point on the graph. Using a table or a graph, identify two points shown.

A parabola is a visual representation of a quadratic function. Each parabola contains a y-intercept, the point at which the function crosses the y-axis. Learn the tools you need to find the y-intercept using the graph of a quadratic function and the equation of a quadratic function. Finding the y-intercept of a parabola can be tricky. Although the y-intercept is hidden, it does exist. Use the equation of the function to find the y- intercept. The y-intercept has two parts: the x-value and the y-value.

Y intercept of parabola

The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry. Determine the vertex, axis of symmetry, zeros, and y -intercept of the parabola shown below. The vertex is the turning point of the graph. The axis of symmetry is the vertical line that intersects the parabola at the vertex. We can use the general form of a parabola to find the equation for the axis of symmetry. The vertex always occurs along the axis of symmetry. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function. If we are given the general form of a quadratic function:.

The vertex always occurs along the axis of symmetry. Question 5: Which equation is represented by the graph below? The correct answer is C.

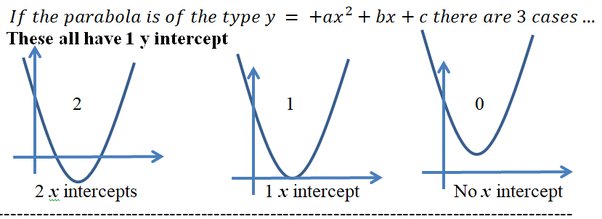
The following graphs are two typical parabolas their x-intercepts are marked by red dots, their y-intercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot:. We say that the first parabola opens upwards is a U shape and the second parabola opens downwards is an upside down U shape. In order to graph a parabola we need to find its intercepts, vertex, and which way it opens. Notice that the x -intercepts of any graph are points on the x -axis and therefore have y -coordinate 0. If the equation factors we can find the points easily, but we may have to use the quadratic formula in some cases. If the solutions are imaginary, that means that the parabola has no x -intercepts is strictly above or below the x -axis and never crosses it.

Two points determine any line. However, since a parabola is curved, we should find more than two points. In this text, we will determine at least five points as a means to produce an acceptable sketch. To begin, we graph our first parabola by plotting points. Choose some values for x and then determine the corresponding y -values. Then plot the points and sketch the graph. When graphing, we want to include certain special points in the graph. The y -intercept is the point where the graph intersects the y -axis.

Y intercept of parabola

A parabola is a visual representation of a quadratic function. Each parabola contains a y-intercept, the point at which the function crosses the y-axis. Learn the tools you need to find the y-intercept using the graph of a quadratic function and the equation of a quadratic function. Finding the y-intercept of a parabola can be tricky. Although the y-intercept is hidden, it does exist.

Sialic

We can use the general form of a parabola to find the equation for the axis of symmetry. So, plug in zero for x and solve for y:. Measure advertising performance. Any number can be the input value of a quadratic function. Answer: The correct answer is A. On this page:. The correct answer is A. If we are given the general form of a quadratic function:. The correct answer is B. One important feature of the graph is that it has an extreme point, called the vertex.

Curved antennas, such as the ones shown in Figure 1 , are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function. In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion.

The domain is all real numbers. Note that the x-value is always zero. CC licensed content, Original. In real life, this often refers to the starting point when something is being measured. Determine the vertex, axis of symmetry, zeros, and y -intercept of the parabola shown below. When a function is in slope-intercept form, the y -intercept can quickly be identified because it is represented by the variable b. Answer: The correct answer is D. Math Glossary: Mathematics Terms and Definitions. You may accept or manage your choices by clicking below, including your right to object where legitimate interest is used, or at any time in the privacy policy page. Any number can be the input value of a quadratic function. Learn about our Editorial Process. Show Solution The vertex is the turning point of the graph. Use the equation of the function to find the y- intercept. Each parabola contains a y-intercept, the point at which the function crosses the y-axis.