Prime factorization of 231

Factors of are the list of integers that we can split evenly into There are total 8 factors of i. Factors of are pairs of those numbers whose products result in

Factors of are any integer that can be multiplied by another integer to make exactly In other words, finding the factors of is like breaking down the number into all the smaller pieces that can be used in a multiplication problem to equal There are two ways to find the factors of using factor pairs, and using prime factorization. Factor pairs of are any two numbers that, when multiplied together, equal Find the smallest prime number that is larger than 1, and is a factor of For reference, the first prime numbers to check are 2, 3, 5, 7, 11, and

Prime factorization of 231

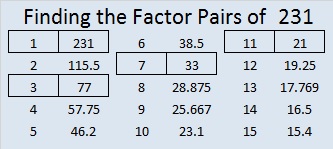
The factors of are numbers that give off zero as the remainder when acts as the divided. Since the number is an odd composite number so it consists of multiple factors. The negative factors of are similar to its positive factors, just with a negative sign. The prime factorization of is the way of expressing its prime factors in the product form. In this article, we will learn about the factors of and how to find them using various techniques such as upside-down division, prime factorization, and factor tree. The factors of are 1, 3, 7, 11, 21, 33, 77, and All of these numbers are the factors as they do not leave any remainder when divided by The factors of are classified as prime numbers and composite numbers. The prime factors of the number can be determined using the technique of prime factorization. You can find the factors of by using the rules of divisibility. The divisibility rule states that any number, when divided by any other natural number, is said to be divisible by the number if the quotient is the whole number and the resulting remainder is zero. To find the factors of , create a list containing the numbers that are exactly divisible by with zero remainders.

Therefore, -1, -3, -7,, and are called negative factors of To find the factor pairs offollow these steps: Step 1: Find the smallest prime number that prime factorization of 231 larger than 1, and is a factor of

Here we have a collection of all the information you may need about the Prime Factors of We will give you the definition of Prime Factors of , show you how to find the Prime Factors of Prime Factorization of by creating a Prime Factor Tree of , tell you how many Prime Factors of there are, and we will show you the Product of Prime Factors of Prime Factors of definition First note that prime numbers are all positive integers that can only be evenly divided by 1 and itself. Prime Factors of are all the prime numbers that when multiplied together equal To get the Prime Factors of , you divide by the smallest prime number possible. Then you take the result from that and divide that by the smallest prime number. Repeat this process until you end up with 1.

The factors of are numbers that give off zero as the remainder when acts as the divided. Since the number is an odd composite number so it consists of multiple factors. The negative factors of are similar to its positive factors, just with a negative sign. The prime factorization of is the way of expressing its prime factors in the product form. In this article, we will learn about the factors of and how to find them using various techniques such as upside-down division, prime factorization, and factor tree.

Prime factorization of 231

How to find Prime Factorization of ? Prime factorization is the process of finding the prime numbers that multiply together to form a given positive integer. In other words, it's the process of expressing a positive integer as a product of prime numbers.

The lion king soundtrack cd

All of these numbers are the factors as they do not leave any remainder when divided by See illustration below. To find the factors of , we will have to find the list of numbers that would divide without leaving any remainder. Now, multiply the resulting exponents together. The factors of are 1, 3, 7, 11, 21, 33, 77, Remember that this new factor pair is only for the factors of 77, not Prime Factors of definition First note that prime numbers are all positive integers that can only be evenly divided by 1 and itself. Maths Puzzles. The possible factor pairs of are given as 1, , 3, 77 , 7, 33 , and 11, The list of all the factors of including positive as well as negative numbers is given below. Our Team. Example 3: Find if 1, 3, 7, 51 and 77 are factors of To set your child on the right path, there are many skills and traits that you can start building and nurturing now.

Looking to get a list of the prime factors of ? In this article we'll give you all of the information you need, including the definition of the prime factors of , how to calculate the prime factors of also known as the prime factorization of

For reference, the first prime numbers to check are 2, 3, 5, 7, 11, and Privacy Policy. This obtained product is equivalent to the total number of factors of the given number. If so, try to find the Prime Factors of the next number on our list and then check your answer here. Our Mission. Prime Factorization of To find the Prime factorization of , we break down all the factors of until we are left with only prime factors. The possible factor pairs of are given as 1, , 3, 77 , 7, 33 , and 11, Negative factors are the additive inverse of the positive factors of a given number. Here are the steps for finding the prime factorization of Step 1: Find the smallest prime number that is larger than 1, and is a factor of Example 1 How many factors of are there?