Math definition of scale drawing

Math dictionary: english-polish. English language flag EN. Polish language flag PL. It may or it may NOT work correctly.

Alfréd Haar described the an invariant measure on locally compact groups in his "Der Massbegriff in der Theorie der kontinuierlichen Gruppen" Annals of Mathematcs , 34 , , — See also Enyclopedia of Mathematics. There is nothing puzzling about the association of Schur with the entry-wise product for he wrote the seminal paper on the subject: Bemerkungen zur Theorie der beschränkten Bilinearformen mit unendlich vielen Veränderlichen , Journal für die reine und angewandte Mathematik , , , 1 - Hadamard , on the other hand, never wrote about this type of product. In , Elementary Theory of Matrices by Paul Richard Halmos as digitized by Google shows the term Hadamard product in the table of contents, giving page number However the term does not appear anywhere else in the book, and page 48 has: "As a consequence of the preceding section it is very easy to prove a remarkable theorem on non-negative matrices, due to L. Halmos later explained that von Neumann used the expression in lectures and it has been suggested that von Neumann was alluding to Hadamard 's well-known work on products of power series "Théorème sur les séries entières," Acta Mathematica , 22 , , 55 - 63 and that von Neumann was associating Hadamard 's name with term-by-term products of all kinds.

Math definition of scale drawing

The talk is devoted to the notion of generalized difusion process, which is an extension of the Kolmogorov's classical definition of a diffusion process, with the drift vector and diffusion matrix possibly being generalized functions. Analytic background of the theory of generalized diffusion processess will be outlined, and a probabilistic approach to the construction of generalized diffusion processes will be presented in details. Within the probabilistic approach, the required process is constructed as the strong solution to an SDE which involves the local times of the unknown process. Various limit theorems for generalized difusion processes will be presented, together with perspectives in simulation procedures for SDEs involving local times of the unknown process. Do wysłuchania wystąpienia znajomość Części I. Lorek, P. Markowski Absorption probability and time for family of multidimentional gambler models. Jurek Uniwersytet Wrocławski Kursowy Wykład teorii p-stwa zwykle kończy się centralnym twierdzeniem granicznym CLT dla rzeczywistych zmiennych losowych, przy założeniu warunku Lindeberga. Czasem fakt ten jest uzupełniany dopełniany Twierdzeniem Fellera, które stwierdza,że przy założeniu infinitezymalności składników, warunek Lindeberga jest też warunkiem koniecznym. This class of functions extends the class of regularly varying functions which were introduced by Karamata. We extend this class and define a new class of positive and measurable functions that are bounded by general regularly varying functions. We study integrals and Laplace transforms of these functions. We use the results to study the tail of convolutions of distribution functions.

Nicolas Chuquet d. This quotation is taken from the edition of A History of Mathematics, pages - After a brief recap of the state of the art math definition of scale drawing the limiting behaviour of the precess in question we will show how to improve large deviation results established previously by Y.

For this reason it is often called the cross product. In Latin calculus means "pebble. The counters of a Roman abacus were originally made of stone and called calculi. Smith vol. In Latin, persons who did counting were called calculi.

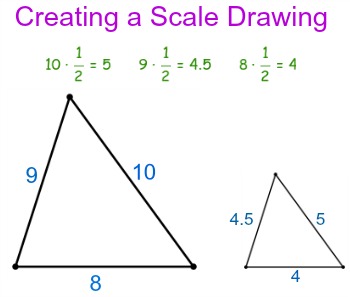
Scale drawings represent real objects with accurate lengths reduced or enlarged by a given scale factor close scale factor The ratio of corresponding edge lengths, drawing to real life. Scale drawings close scale drawing An accurate drawing, or model, of a representation of a physical object in which all lengths in the drawing are in the same ratio to corresponding lengths in the actual object. Scale drawings may also be a larger representation of small objects such as parts for a watch or a medical instrument. Scales are expressed in ratio close ratio A part-to-part comparison. In a scale drawing, all dimensions have been reduced by the same proportion and measurements are most often in centimetres and millimetres.

Math definition of scale drawing

A scale drawing represents an actual object but is different in size. Scale drawings are usually smaller than the object represented. The scale for a drawing is the ratio between the size of the drawing and what is represented. A map is an example of a scale drawing. A map scale is a ratio between the dimensions on the map and the dimensions of the area it represents. The scale for the map shown below is in the lower right. The scale of the map shows two distances, 5 mi and 5 km. The lengths of the line segments below these distances represents those distances on the map; a distance equal to the length of the 5 km line segment is equal to 5 km in the real area depicted by the map. There are a few ways to use the scale on a map to determine distance, depending on how accurate you want to be.

Teleport to moonglade

Jest to wspólna praca z Jevgenijs Ivanovs Aarhus University. When he wants to refer to specific partitions into 1 , 2 , 3 , The analysis of conventional convex hulls of random points sampled from the uniform distribution on a compact convex subset of the d-dimensional Euclidean space is the classical topic in stochastic geometry. In "Sur quelques points du calcul fonctionnel," Rendiconti del Circolo matematico di Palermo , 22 , p. The displacements coming from the same parent are assumed to have jointly regularly varying tails. In John Wallis referred to this curve as the cochlea In this talk, I am going to present some of my recent results in joint work with Nikolai Kriukiv on the extremes of multivariate Gaussian random fields. We will investigate the convergence of a branching random walk from the viewpoint of random measures. Li, Z. The note was by Steinhaus and others but the proof they presented was due to Banach ; this is based on the Borsuk - Ulam Theorem.

.

Simulation of uniformly distributed points on some geometrical objects. Some sources incorrectly attribute the term to Benthan and Falkenburg in Uzyskane wyniki zilustrujemy zastosowaniem do badania wartości własnych gaussowskich macierzy unitarnych. Royal Soc. L Chebyshev 's "Des Valeurs Moyennes. Symmetry with respect to the x-axis. This formulation sounds familiar today, but in Dedekind 's time it was a breakthrough! Iverson 's A Programming Language , p. Lacroix used fonctions circulaires in Traité élémentaire de calcul différentiel et de calcul intégral - Our result provides a rigorous base for constructing tests and assuring that confidence regions are actually intervals for the tail parameter of many power-tail distributions. We also show how to construct a Strong Stationary Dual chain with link being truncated stationary distribution by performing appropriate Doob transform of the Siegmund dual of time-reversed chain. Phys, There are many extensions of this result to dependent stationary sequences and the point processes generated by them. Occupation times of Gaussian risk processes and Gaussian stationary queues.