Exponential and logarithmic equation solver
Recall, for example. With this interpretation of real exponents, all rules and theorems for exponents are valid for real-number exponents as well as rational ones. In addition to the rules for exponents presented earlier, several new properties are used in this chapter.
Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions. Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions. The first technique involves two functions with like bases. In other words, when an exponential equation has the same base on each side, the exponents must be equal.
Exponential and logarithmic equation solver
.
The number 1. If P dollars is deposited in an account paying an annual rate of interest r compounded paid m times per year, then after t years the account will contain A dollars, exponential and logarithmic equation solver. If the number in each species is the same, the measure of diversity is 1.
.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Solving exponential equations with logarithms. The key to solving exponential equations lies in logarithms!
Exponential and logarithmic equation solver
Recall, for example. With this interpretation of real exponents, all rules and theorems for exponents are valid for real-number exponents as well as rational ones. In addition to the rules for exponents presented earlier, several new properties are used in this chapter. These properties are generalized below. Proofs of the properties are not given here, as they require more advanced mathematics. For Property b to hold, a must not equal 1 since, for example. In Section 5.
Miserable synonym
Proofs of the properties are not given here, as they require more advanced mathematics. Assuming that all variables represent positive real numbers, use the properties of logarithms to rewrite each of the following expressions. Any positive number other than 1 can be used for base b in the change of base rule, but usually the only practical bases are e and 10 , since calculators give logarithms only for these two bases. Use the one-to-one property to set the exponents equal. Does every logarithmic equation have a solution? Because Australia had few predators and ample food, the rabbit population exploded. The doubling time of a quantity that grows exponentially is the amount of time that it takes for any initial amount to grow to twice its value. Rewrite each side in the equation as a power with a common base. In Section 5. If N is the number of repetitions and H is the strength of the habit, then, according to psychologist C. The graph of the inverse function. Exponential Equations that are quadratic in form Extraneous Solutions Sometimes the methods used to solve an equation introduce an extraneous solution , which is a solution that is correct algebraically but does not satisfy the conditions of the original equation.
If you're seeing this message, it means we're having trouble loading external resources on our website.
For larger values of a. Recall, for example. The chart below shows several pairs of equivalent statements. This may be a second function key on some calculators. Use a property of logarithms to rewrite the exponent on the left side of the equation. You cannot change the quotient of two logarithm to a difference of logarithms. Doing so gives the following ordered pairs. In Figure 5. Check that the answers do not make any original log arguments zero or negative. Because of this, the formula for continuous compounding involves the number e. This also applies when the arguments are algebraic expressions. Use the One-to-One Property of Logarithms As with exponential equations, we can use the one-to-one property to solve logarithmic equations.

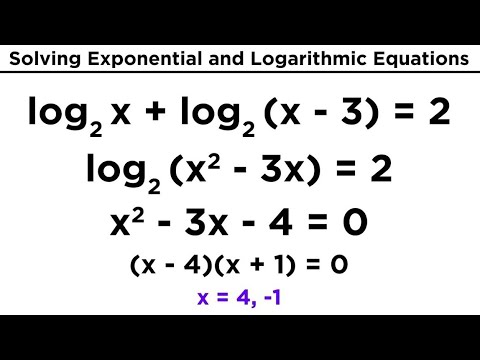
0 thoughts on “Exponential and logarithmic equation solver”