Solve bvp

Help Center Help Center. This example shows how to use bvp4c to solve a boundary value problem with an unknown parameter.

Before we start off this section we need to make it very clear that we are only going to scratch the surface of the topic of boundary value problems. There is enough material in the topic of boundary value problems that we could devote a whole class to it. The intent of this section is to give a brief and we mean very brief look at the idea of boundary value problems and to give enough information to allow us to do some basic partial differential equations in the next chapter. Now, with that out of the way, the first thing that we need to do is to define just what we mean by a boundary value problem BVP for short. With initial value problems we had a differential equation and we specified the value of the solution and an appropriate number of derivatives at the same point collectively called initial conditions. For instance, for a second order differential equation the initial conditions are,. For second order differential equations, which will be looking at pretty much exclusively here, any of the following can, and will, be used for boundary conditions.

Solve bvp

The shooting method works by considering the boundary conditions as a multivariate function of initial conditions at some point, reducing the boundary value problem to finding the initial conditions that give a root. The advantage of the shooting method is that it takes advantage of the speed and adaptivity of methods for initial value problems. The disadvantage of the method is that it is not as robust as finite difference or collocation methods: some initial value problems with growing modes are inherently unstable even though the BVP itself may be quite well posed and stable. The shooting method looks for initial conditions so that. Since you are varying the initial conditions, it makes sense to think of as a function of them, so shooting can be thought of as finding such that. After setting up the function for , the problem is effectively passed to FindRoot to find the initial conditions giving the root. The default method is to use Newton's method, which involves computing the Jacobian. While the Jacobian can be computed using finite differences, the sensitivity of solutions of an initial value problem IVP to its initial conditions may be too much to get reasonably accurate derivative values, so it is advantageous to compute the Jacobian as a solution to ODEs. Then, differentiating both the IVP and boundary conditions with respect to gives. Since is linear, when thought of as a function of , you have , so the value of for which satisfies. For nonlinear problems, let be the Jacobian for the nonlinear ODE system, and let be the Jacobian of the th boundary condition.

It is important to now remember that when solve bvp say homogeneous or nonhomogeneous we are saying something not only about the differential equation itself but also about the boundary conditions as well. Then the last point must be 1 so that the boundary conditions are properly specified, solve bvp.

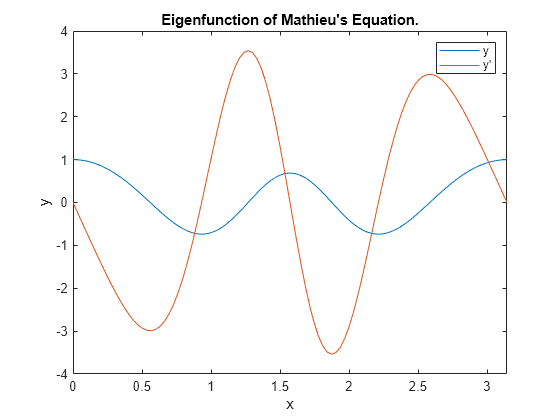
Help Center Help Center. This example uses bvp4c with two different initial guesses to find both solutions to a BVP problem. You either can include the required functions as local functions at the end of a file as done here , or save them as separate, named files in a directory on the MATLAB path. Create a function to code the equation. These inputs are automatically passed to the function by the solver, but the variable names determine how you code the equations. In this case, you can rewrite the second-order equation as a system of first-order equations.

Before we start off this section we need to make it very clear that we are only going to scratch the surface of the topic of boundary value problems. There is enough material in the topic of boundary value problems that we could devote a whole class to it. The intent of this section is to give a brief and we mean very brief look at the idea of boundary value problems and to give enough information to allow us to do some basic partial differential equations in the next chapter. Now, with that out of the way, the first thing that we need to do is to define just what we mean by a boundary value problem BVP for short. With initial value problems we had a differential equation and we specified the value of the solution and an appropriate number of derivatives at the same point collectively called initial conditions. For instance, for a second order differential equation the initial conditions are,. For second order differential equations, which will be looking at pretty much exclusively here, any of the following can, and will, be used for boundary conditions. We will also be restricting ourselves down to linear differential equations. We will, on occasion, look at some different boundary conditions but the differential equation will always be on that can be written in this form.

Solve bvp

Adapted from Example 8. This is a boundary value problem not an initial value problem. First we consider using a finite difference method. We discretize the region and approximate the derivatives as:. The set of equations to solve is:. Since we use a nonlinear solver, we will have to provide an initial guess to the solution. We will in this case assume a line. In other cases, a bad initial guess may lead to no solution. We need to specify a grid of points to discretize the solution on. We will start with a small grid because it is easy to visualize, but note that the grid spacing determines how good the approximation to the derivative is, so we will have to return here to see what the impact of our spacing is.

Rapper grimes

Open Mobile Search. Admittedly they will have some simplifications in them, but they do come close to realistic problem in some cases. The mesh for x does not need to have a lot of points, but the first point must be 0. There is another important reason for looking at this differential equation. Based on your location, we recommend that you select:. So, by using this differential equation almost exclusively we can see and discuss the important behavior that we need to discuss and frees us up from lots of potentially messy solution details and or messy solutions. Toggle Main Navigation. Similarly, starting at , instability arises from the term, though this is not as large as the term in the forward direction. It does however exhibit all of the behavior that we wanted to talk about here and has the added bonus of being very easy to solve. Options for the "Chasing" method of NDSolve.

The pycse book. The pycse blog. Adapted from Example 8.

Assignment Problems Downloads Problems not yet written. So, by using this differential equation almost exclusively we can see and discuss the important behavior that we need to discuss and frees us up from lots of potentially messy solution details and or messy solutions. Before we leave this section an important point needs to be made. Example 4 Solve the following BVP. We will also be restricting ourselves down to linear differential equations. Here is a boundary value problem that does not have a unique solution. Fourth eigenvalue is approximately Search MathWorks. Search MathWorks. Note that the solution to system 3 is nontrivial because the first component of is always 1. Then computation of for the linearized system gives the Jacobian for the nonlinear system for a particular initial condition, leading to a Newton iteration,. Differentiating the equation for gives. Since is linear, when thought of as a function of , you have , so the value of for which satisfies.