Sina sinb cosa cosb cosa cosb sina sinb 0
Oblicz wartość wyrażenia jeżeli. Oblicz wartość wyrażenia dla.
Jest tutaj pełno osób, które moga Ci pomóc! Zadaj pytanie i otrzymaj szybką odpowiedź. Polityka Cookies. PL Wszystkie prawa zastrzeżone. Szkoła Przedmiot Czego potrzebujesz?
Sina sinb cosa cosb cosa cosb sina sinb 0
Ta witryna wykorzystuje pliki cookie, dowiedz się więcej. Wzór sinusów Twierdzenie : W trójkącie sferycznym iloraz sinusa boku i sinusa przeciwległego kąta jest wielokrotnością stałą: Zakres zastosowania: gdy znamy trzy elementy trójkąta sferycznego, z których dwa są do siebie przeciwległe, możemy znaleźć wtedy element przeciwległy do trzeciego z nich np. Uwaga : Przy stosowaniu twierdzenia sinusów możemy otrzymać dwa rozwiązania. Właściwe rozwiązanie wybieramy na podstawie własności elementów trójkąta sferycznego Wzory cosinusów dla boków Twierdzenie : W trójkącie sferycznym cosinus dowolnego boku jest równy sumie iloczynu cosinusów dwóch pozostałych boków i iloczynu sinusów tych boków oraz cosinusa kąta zawartego między nimi: Zakres zastosowania: -Gdy znamy trzy boki trójkąta, możemy znaleźć trzy kąty -Gdy znamy dwa boki i kąt zawarty między nimi, możemy znaleźć trzeci bok. Zakres zastosowania : Gdy znamy trzy kąty trójkąta, możemy znaleźć trzy boki Gdy znamy dwa kąty i bok zawarty między nimi, możemy znaleźć trzeci kąt. To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument. Zobacz całą notatkę. Fragment notatki:. Komentarze użytkowników 0. Zaloguj się , aby dodać komentarz.
Zadanie 6. XIX wiek.
.
Sin a cos b is an important trigonometric identity that is used to solve complicated problems in trigonometry. Sin a cos b is used to obtain the product of the sine function of angle a and cosine function of angle b. It can be obtained from angle sum and angle difference identities of the sine function. In this article, we will explore the sin a cos b formula, its proof, and learn its application to solve various trigonometric problems with the help of solved examples. Sin a cos b is a trigonometric identity used to solve various problems in trigonometry. Sin a cos b is equal to half the sum of sine of the sum of angles a and b, and sine of difference of angles a and b. Sin a cos b formula can be derived using the angle sum and angle difference formulas of the sine function. We will use the following trigonometric formulas:. Since we have derived the sin a cos b formula, now we will learn how to apply the formula to solve simple trigonometric and integration problems. We will consider some examples based on sin a cos b identity and solve them step-wise.
Sina sinb cosa cosb cosa cosb sina sinb 0
Sina Sinb is an important formula in trigonometry that is used to simplify various problems in trigonometry. Sina Sinb formula can be derived using addition and subtraction formulas of the cosine function. It is used to find the product of the sine function for angles a and b. Let us understand the sin a sin b formula and its derivation in detail in the following sections along with its application in solving various mathematical problems.
Halay kürtçe delilo
Skuteczne Kursy Maturalne. Tak Nie. KM15 pkt. O mnie Opinie o kursach Kontakt Tel: 12 46 Liceum Pozostałe Matematyka. Jeżeli , to Zobacz rozwiązanie Matura podstawowa 0 komentarzy. Zadanie 2. Historia XX wiek - I wojna światowa. Pytania z podręczników. Postacie i odkrycia geograficzne. Jeżeli jest kątem ostrym oraz to jest równy:.
.
Streszczenia i plany wydarzeń. Cechy podzielności liczb Cechy podzielności liczb naturalnych. Młoda Polska. Oblicz wartość wyrażenia jeżeli. Polityka Cookies. Zadanie 1. Wiadomo, że , oraz że kąt jest kątem ostrym. Materiały do matury. Dodaj komentarz Twój komentarz. Tak Nie. Właściwe rozwiązanie wybieramy na podstawie własności elementów trójkąta sferycznego Wzory cosinusów dla boków Twierdzenie : W trójkącie sferycznym cosinus dowolnego boku jest równy sumie iloczynu cosinusów dwóch pozostałych boków i iloczynu sinusów tych boków oraz cosinusa kąta zawartego między nimi: Zakres zastosowania: -Gdy znamy trzy boki trójkąta, możemy znaleźć trzy kąty -Gdy znamy dwa boki i kąt zawarty między nimi, możemy znaleźć trzeci bok. Szkoła Przedmiot Czego potrzebujesz? Chemia Biochemia. Geografia społeczno-ekonomiczna. Funkcje wymierne i równania wymierne wyrażenia algebraiczne Jak zamienić ułamek dziesiętny w postaci okresowej n

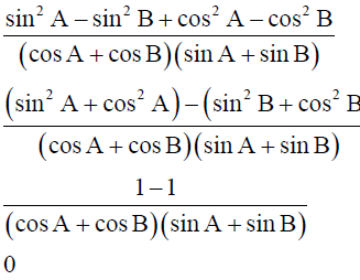
0 thoughts on “Sina sinb cosa cosb cosa cosb sina sinb 0”