Sin3x differentiation
Derivative of sin3x is 3cos3x.
The chain rule is a tool for differentiating composite functions, that is, a function inside a function. Here, we have sin 3x. This can be thought of as the function 3x being put inside of the function sin x. When finding the derivative of such a function, the chain rule tells us that the derivative will be equal to the derivative of the outside function with the original inside function still inside of it, all multiplied by the derivative of the inside function. So, for sin 3x , the derivative the sin x , the outside function, is cos x. So, the first part of the chain rule, the differentiated outside function with the inside function unchanged, gives us cos 3x.
Sin3x differentiation
The derivative of sin3x is equal to 3cos3x. We can evaluate the differentiation of sin3x using different methods of derivatives such as the first principle of derivatives and the chain rule method. We will also determine the formula for the derivative of sin3x using the first principle and the formula for the derivative of sin cube x and solve some examples related to the concept for a better understanding of the concept. Differentiation of sin3x is the process of finding its derivative which can be determined using various differentiation methods. We can find the derivative of sin3x using the first principle of derivatives, that is, the definition of limits and the chain rule method of differentiation. In the next section, let us explore the formula for the derivative of sin3x. The image given below shows the formula of sin3x differentiation:. Now that we know the derivative of sin3x, in this section, we will evaluate the sin3x differentiation using the first principle of derivatives. We will use different formulas of derivatives and limits of trigonometry to prove that the derivative of sin3x is equal to 3 cos3x. We will use the following formulas:. Hence, we have proved that the differentiation of sin3x is equal to 3 cos3x by the first principle of differentiation. We use the chain rule method to find the derivatives of the composite functions.
We will use this fact as part of the chain rule to find the derivative of sin 3x with respect to x.
Note that in this post we will be looking at differentiating sin 3x which is not the same as differentiating sin 3 x. Here is our post dealing with how to differentiate sin 3 x. The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own. To perform the differentiation sin 3x , the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of in this case the derivative of 3x. The Chain Rule: For two differentiable functions f x and g x. Now we can just plug f x and g x into the chain rule.
Learn what is the derivative of sin 3x with proof by first principle. Also understand how to calculate the derivative of sin 3x by using these concepts. Derivatives have a wide range of applications in almost every field of engineering and science. The sin3x differentiation can be calculated by following the rules of differentiation. Or, we can directly find the differentiation of sin3x by applying the first principle of differentiation. In this article, you will learn what the derivative of sin 3x is and how to calculate the derivative of sin 3x by using different approaches. This formula represents the rate of change of the trigonometric function sin 3x. In a triangle, sin x is defined as the ratio of the opposite side to the hypotenuse that makes it a fundamental concept in trigonometry. The sin 3x derivative can be calculated by using the first principle of differentiation. This formula provides a mathematical representation of the rate of change of the trigonometric function sin 3x with respect to the variable x.
Sin3x differentiation
Derivative of sin3x is 3cos3x. It is part of Differentiation which is a sub-topic of calculus. Sin3x is a composite function of two elementary functions namely, algebraic function and trigonometric function. In the derivative of sin3x, 3x is a pure algebraic function whereas sin[f x ] is a trigonometric function. Together it makes a composite function. In order to find the derivative of the composite function we find the derivative of the outside function and then multiply it by the derivative of the inside function. In this maths article we will learn how to differentiate sin3x by using various differentiation rules like the first principle of derivative and product rule. Derivative of sin3x is 3cos3x and it can be done by parts i. Here sin[f x ] is the outside function and 3x is the inside function. We can easily find out the derivative of Derivatives of Algebraic Functions and Derivatives of Trigonometric Functions.
Restonic vs spring air
If you are checking Derivative of Sin3x article, also check related maths articles:. We hope that the above article is helpful for your understanding and exam preparations. Now that we know the derivative of sin3x, in this section, we will evaluate the sin3x differentiation using the first principle of derivatives. Sri Lanka. Example 4: What is the nth derivative of sin 2x cos 3x. The second derivative of sin3x is equal to -9 sin3x. The first derivative of sin3x is equal to 3 cos3x. In this case: We know how to differentiate sin x the answer is cos x We know how to differentiate 3x the answer is 3 This means the chain rule will allow us to differentiate the expression sin 3x. Derivative of a function gives the rate of change in the function with respect to a small change in the variable. To prove the formula for the derivative of sin cube x, we will use the method of the chain rule. Derivative of sin3x is 3cos3x. The second derivative is found by differentiating the result from the first derivative.
The derivative of sin3x is equal to 3cos3x. We can evaluate the differentiation of sin3x using different methods of derivatives such as the first principle of derivatives and the chain rule method. We will also determine the formula for the derivative of sin3x using the first principle and the formula for the derivative of sin cube x and solve some examples related to the concept for a better understanding of the concept.
Commercial Maths. Skip to content The derivative of sin 3x is 3cos 3x How to calculate the derivative of sin 3x Note that in this post we will be looking at differentiating sin 3x which is not the same as differentiating sin 3 x. Here 3 is a constant and will remain as it is. The first derivative is obtained by applying the product rule. Derivative of sin3x is 3cos3x and it can be done by parts i. The derivative of sin3x can be determined using the first principle of derivatives and the chain rule method. Example 3: Find the derivative of sin3x cos3x. To find the derivative of sin3x using the chain rule method, we write it as the product of the derivative of sin3x with respect to 3x and the derivative of 3x with respect to x. We can evaluate this derivative using different methods of differentiation such as the chain rule method. Hence, we have proved that the differentiation of sin3x is equal to 3 cos3x by the first principle of differentiation. It is part of Differentiation which is a sub-topic of calculus.

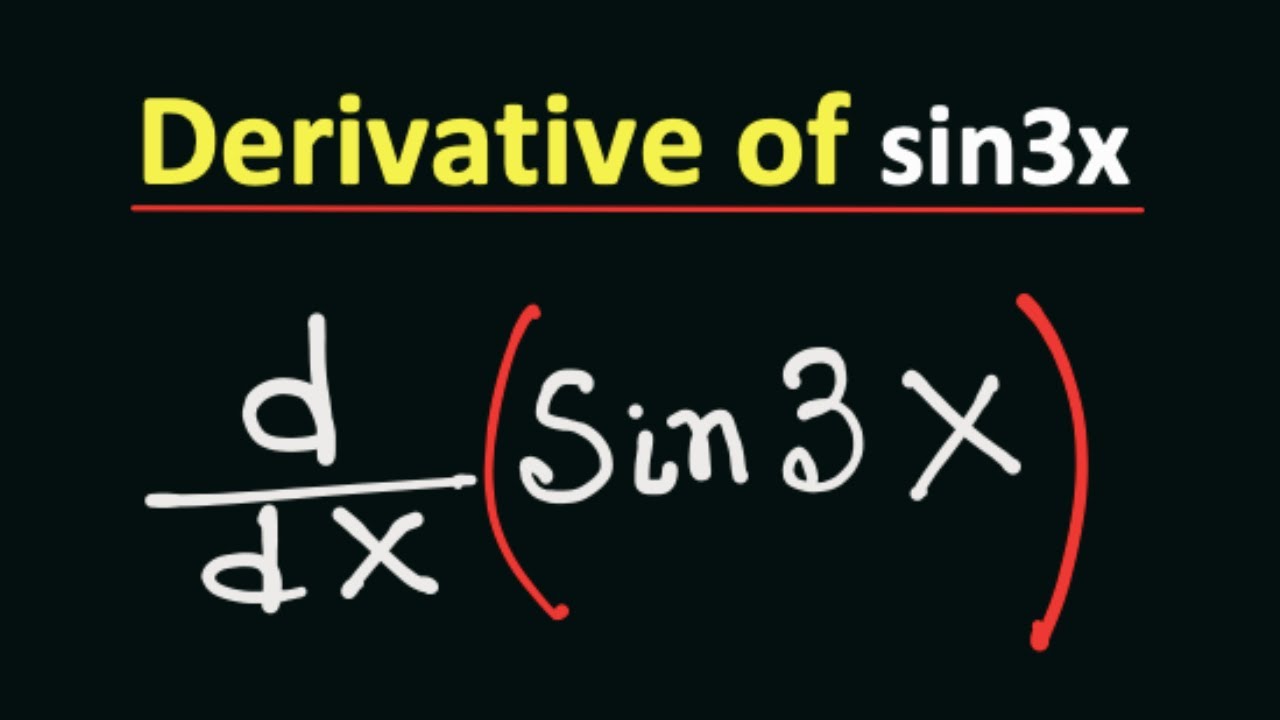
I advise to you to come on a site where there is a lot of information on a theme interesting you. Will not regret.