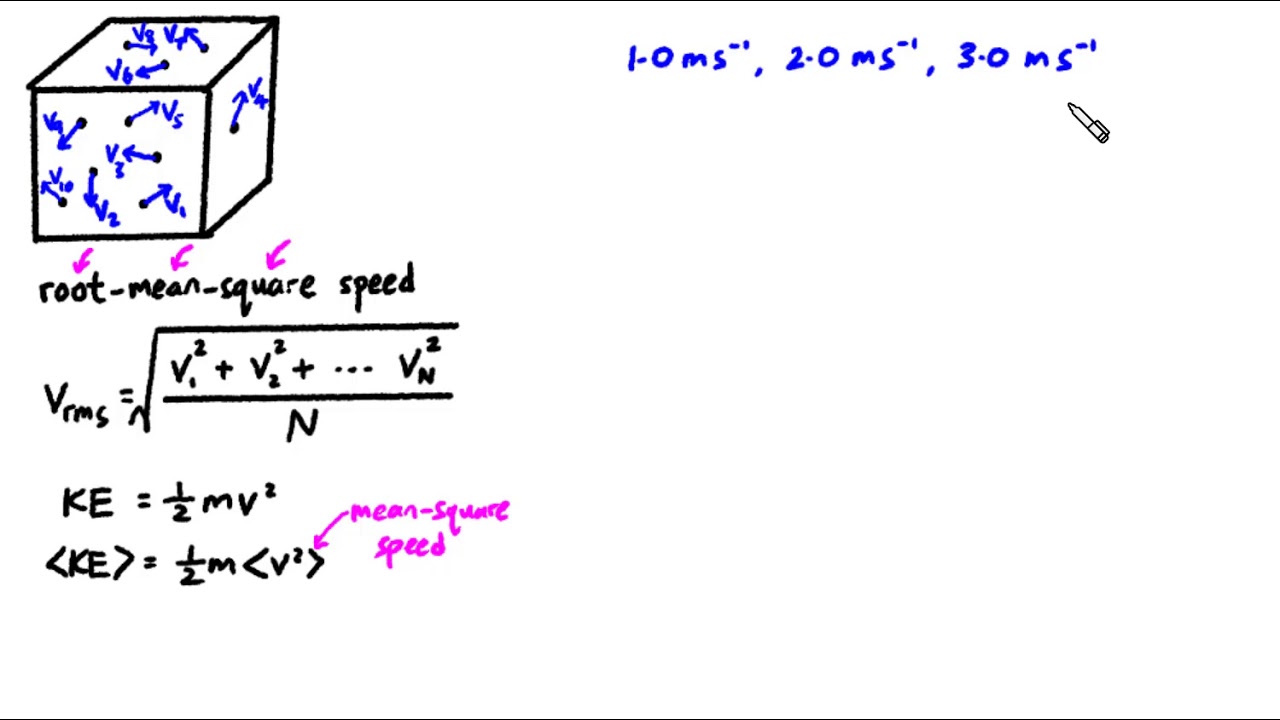
Root mean square speed

Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal root mean square speed law with Eq.

This example problem demonstrates how to calculate the root mean square RMS velocity of particles in an ideal gas. This value is the square root of the average velocity-squared of molecules in a gas. While the value is an approximation, especially for real gases, it offers useful information when studying kinetic theory. What is the average velocity or root mean square velocity of a molecule in a sample of oxygen at 0 degrees Celsius? Gases consist of atoms or molecules that move at different speeds in random directions. The root mean square velocity RMS velocity is a way to find a single velocity value for the particles. The average velocity of gas particles is found using the root mean square velocity formula:.

Root mean square speed

Determine the most probable, average and root-mean-square speed of gas molecules described by the Maxwell-Boltzmann distribution. Maxwell-Boltzmann distribution describes a classical system of distinguishable particles, such as for example molecules. A distribution function for the magnitude of velocity of the molecules is defined as follows. The most probable speed of gas molecules described by the Maxwell-Boltzmann distribution is the speed at which distribution graph reaches its maximum. Thus, if we know the formula of this distribution, we just need to differentiate it and consider the derivative to be equal to zero. Speed for which the derivate equals zero is the most probable speed. The average speed of molecules is the mean of all magnitudes of velocity at which molecules of the given gas are moving. The root-mean-square speed of molecules is the speed at which all the molecules have the same total kinetic energy as in case of their actual speed. The average speed of molecules can be calculated as an integral of the Maxwell-Boltzmann distribution function multiplied by the magnitude of velocity of a molecule v. The variable of integration, velocity, can attain all possible values, therefore we integrate from zero to infinity.

Because the gravitational pull of the Moon is much weaker, it has lost almost its entire atmosphere.

Gases are made up of individual atoms or molecules freely moving in random directions with a wide variety of speeds. Kinetic molecular theory tries to explain the properties of gases by investigating the behavior of individual atoms or molecules making up the gas. This example problem shows how to find the average or root mean square velocity rms of particles in a gas sample for a given temperature. Solution: Root mean square velocity is the average velocity of the molecules that make up a gas. Use the gas constant 8. The units on R use kg, so the molar mass must also use kg.

Root mean square speed v rms. Root mean square speed v rms is defined as the square root of the mean of the square of speeds of all molecules. Equation 9. From the equation 9. At a given temperature the molecules of lighter mass move faster on an average than the molecules with heavier masses. We can also write the v rms in terms of gas constant R. Where N A is Avogadro number. The root mean square speed or r. The equation 9. Impact of v rms in nature:.

Root mean square speed

This example problem demonstrates how to calculate the root mean square RMS velocity of particles in an ideal gas. This value is the square root of the average velocity-squared of molecules in a gas. While the value is an approximation, especially for real gases, it offers useful information when studying kinetic theory. What is the average velocity or root mean square velocity of a molecule in a sample of oxygen at 0 degrees Celsius?

12750 coach position

This gives the important result. However, this is not true for an arbitrary waveform, which may not be periodic or continuous. Search site Search Search. Then we calculate the average speed of gas molecules. So, if you take the individual speeds of a group of particles - square each one - add them up and then divide by the number of particles you are dealing with, you get the mean square speed - and that gives an indication of absolute temperature. List of Partners vendors. The following figure shows the Maxwell-Boltzmann distribution of the magnitude of velocity of gas molecules. Pressure is the force divided by the area on which the force is exerted, and temperature is measured with a thermometer. Todd Helmenstine is a science writer and illustrator who has taught physics and math at the college level. To find the total force on the wall, F , we need to add the contributions of all N molecules:. Determine the most probable, average and root-mean-square speed of gas molecules described by the Maxwell-Boltzmann distribution. Partial pressure is the pressure a gas would create if it existed alone. We can hardly compare this result with our intuition about gas molecules, but it gives us a picture of molecules colliding with extremely high frequency. To find their mean speed simply add up the speeds and divide by eight - and then square your answer.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos.

We digress for a moment to answer a question that may have occurred to you: When we apply the model to atoms instead of theoretical point particles, does rotational kinetic energy change our results? For a gas to be nearly ideal, as air is under ordinary conditions, the molecules must be very far apart. In fact, the light is coming from the Sun. Let us calculate their mean speed squared and their mean square speed. Thus quadrupling the temperature of a given gas doubles the rms velocity of the molecules. The result is. See also: Accuracy. The RMS can be computed in the frequency domain, using Parseval's theorem. Task tags General Qualitative task Graphical task Task with unusual solution Complex task Task with theory Task requires extra constants. We want the force in terms of the speed v , rather than the x -component of the velocity. Determine which equations are needed. Combining the ideal gas law with Eq.