Ordered pair definition for math

An ordered pair refers to two numbers written in a certain order. We generally use ordered pairs in the context of coordinates of a point in a 2D plane. It helps to locate or plot a point easily on a Cartesian plane.

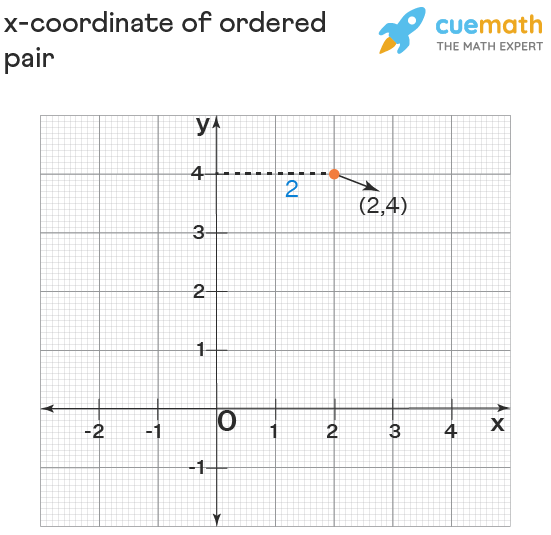
An ordered pair, as its name suggests, is a pair of elements that have specific importance for the order of their placements. Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation. An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parantheses. For example, x, y represents an ordered pair, where 'x' is called the first element and 'y' is called the second element of the ordered pair. These elements have specific names according to what context they are being used and they can be either variables or constants.

Ordered pair definition for math

In mathematics , an ordered pair a , b is a pair of objects. Ordered pairs are also called 2-tuples , or sequences sometimes, lists in a computer science context of length 2. Ordered pairs of scalars are sometimes called 2-dimensional vectors. Technically, this is an abuse of terminology since an ordered pair need not be an element of a vector space. The entries of an ordered pair can be other ordered pairs, enabling the recursive definition of ordered n -tuples ordered lists of n objects. For example, the ordered triple a , b , c can be defined as a , b , c , i. In the ordered pair a , b , the object a is called the first entry , and the object b the second entry of the pair. Alternatively, the objects are called the first and second components , the first and second coordinates , or the left and right projections of the ordered pair. Cartesian products and binary relations and hence functions are defined in terms of ordered pairs, cf. The a , b notation may be used for other purposes, most notably as denoting open intervals on the real number line. In such situations, the context will usually make it clear which meaning is intended. In some introductory mathematics textbooks an informal or intuitive definition of ordered pair is given, such as. For any two objects a and b , the ordered pair a , b is a notation specifying the two objects a and b , in that order.

This "definition" is unsatisfactory because it is only descriptive and is based on an intuitive understanding of order. Short: [13]. Let us learn more about ordered pairs along with its definition, meaning, properties, and more.

.

Their order of appearance is important, so we call them first and second elements respectively. For a complicated problem, divide it into smaller tasks and solve each one separately. Then assemble them to form the final answer. Cartesian products can be extended to more than two sets. Can you explain why? Consider the first identity as an example. The argument we used in the proof is called multiplication principle. We shall study it again in Chapter 7. In brief, it says that if a job can be completed in several steps, then the number of ways to finish the job is the product of the number of ways to finish each step. This idea of one-to-one correspondence is a very important concept in mathematics.

Ordered pair definition for math

Ordered pairs are sets of numbers used for plotting points. They are always written inside parentheses, and are separated by a comma. Ordered pairs are usually seen together with a four-quadrant graph also called a coordinate plane.

Reddit pc master

Each of the 4 parts is known as a quadrant. Mathematical logic. The order of the elements has a certain importance in an ordered pair. An ordered pair is of the form x, y. Ordered Pair An ordered pair, as its name suggests, is a pair of elements that have specific importance for the order of their placements. Already booked a tutor? Our Journey. Elsevier BV. Let us learn more about ordered pairs along with its definition, meaning, properties, and more. Then the point on the graph looks like this. Barkley Rosser , Equality Property of Ordered Pairs 7.

The Cartesian plane is formed by the intersection of two number lines. We use these two number lines to mark points on t his plane. The use of these points is important because they represent specific data points on the plane and indicate relationships in the data represented by the two intersecting number lines.

Our Team. The Kuratowski definition does not allow this. This definition works only if the set of natural numbers is infinite. We call the horizontal axis the x-axis and the vertical axis the y-axis. Equality Property of Ordered Pairs 7. Set theory. Hence if the ordered pair is not taken as primitive, it must be defined as a set. The Quine—Rosser definition above also admits proper classes as projections. Jena: Verlag Hermann Pohle. What is a 2-tuple? For example, 1, 2 is an ordered pair. A Theory of Sets.