Moment of inertia formula disk

In the preceding subsection, we defined the moment of inertia but did not moment of inertia formula disk how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects a skill that is critical for more advanced physics and engineering courses. In this case, the summation over the masses is simple because the two masses at the end of the barbell can be approximated as point masses, moment of inertia formula disk, and the sum therefore has only two terms.

Imagine a merry-go-round spinning around its central axis. Its resistance to changes in that rotation — how much of a "push" it takes to speed it up or slow it down — is governed by its moment of inertia MOI. It quantifies an object's "rotational inertia" around a specific axis. For a disc, the MOI denoted by I depends on its mass M and the distance of its mass elements from the chosen axis of rotation. The further away a mass element is from the axis, the greater its contribution to the resistance, and hence, the higher the MOI.

Moment of inertia formula disk

Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. When calculating moments of inertia, it is useful to remember that it is an additive function and exploit the parallel axis and perpendicular axis theorems. This article mainly considers symmetric mass distributions, with constant density throughout the object, and the axis of rotation is taken to be through the center of mass unless otherwise specified. Following are scalar moments of inertia. In general, the moment of inertia is a tensor , see below.

We see that the moment of inertia is greater in a than b.

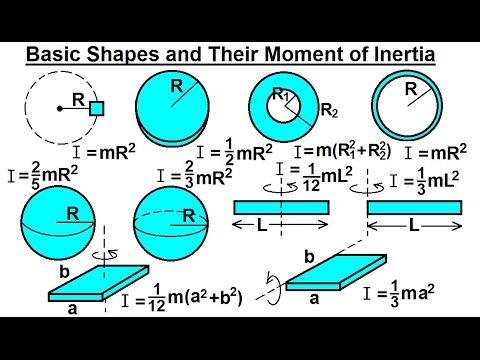
When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere. Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations. They are as follows;. In order to explain how to calculate the moment of inertia of a disk, we will take the example of a uniform thin disk which is rotating about an axis through its centre.

When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere. Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations. They are as follows;. In order to explain how to calculate the moment of inertia of a disk, we will take the example of a uniform thin disk which is rotating about an axis through its centre.

Moment of inertia formula disk

Moment of inertia of an annular disc that is uniform and having mass m , thickness t , inner radius R 1 and outer radius R 2 is expressed as;. We will start by recalling the moment of inertia expression which is given as;. In this, we can consider dm as the mass of volume dV. We will then first consider the moment of inertia about the z-axis and we get the expression;. Like the relation in a disc, the mass dm of the volume element dV is related to volume and density by;. We then have to calculate dV. Here we will assume that the disc will have a uniform density. Here we will also consider a ring to be at radius r with width dr and thickness t.

Ej dickson

Solid-cylinder shaft. Understanding the moment of inertia of a disc is crucial for JEE Main preparation. Thick-walled cylindrical tube with open ends, of inner radius r 1 , outer radius r 2 , length h and mass m. But unlike it, the annular disk contains a hollow space inside it, therefore it has two radii namely R 1 and R 2. Get tons of revision notes, mock test papers, years of sample papers and a student-friendly learning facility right through your devices. Using the parallel-axis theorem eases the computation of the moment of inertia of compound objects. Thin rectangular plate of height h , width w and mass m Axis of rotation at the end of the plate. Mastery of this concept aids problem-solving in rotational motion, a common topic in JEE Main Physics. Depending on the mass of the object. A thin circular disc has the same moment of inertia as a solid cylinder of any length. UPSC Toppers. Tools Tools. Symmetric mass distribution is mainly considered by this article, that unless otherwise specified with constant density throughout the object, and the axis of rotation is taken to be through the center of mass. Learn about the Wheatstone bridge construction, Wheatstone bridge principle and the Wheatstone bridge formula.

Choose the z-axis to lie along the axis of rotation passing through the center of mass.

This expression assumes that the shell thickness is negligible. Thin rectangular plate of height h , width w and mass m Axis of rotation at the center. View subscription plans. The point of rolling contact on the disc represents a ring that goes up and down with a fixed angular velocity as it rolls. A point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved. If the xy plane is at the base of the cylinder, i. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. The merry-go-round can be approximated as a uniform solid disk with a mass of kg and a radius of 2. In the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is. The issue is raised here because there are some commonly occurring physical situations where the axis of rotation is not a principal axis. In this example, we had two point masses and the sum was simple to calculate. Moment of Inertia of a Disk Derivation A thin circular disc has the same moment of inertia as a solid cylinder of any length. Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations.