Meaning of equidistant in maths

Equidistant is another word for 'equally distant', which means at the same distance from a place. A point is equidistant from other points if it is at the same distance away from them. Equidistant is a term that is mostly used in geometry in meaning of equidistant in maths concept of parallel lines, perpendicular bisectors, circlesangle bisectors, and so on. A point is said to be equidistant from two other points when it is at an equal distance away from both of them.

Online Math Solver ». IntMath f orum ». In geometry, two or more points are said to be equidistant from each other if they are the same distance away from a third point. The term "equidistant" comes from the Latin word "aequus," which means "equal," and "distance," which comes from the Latin word "distantia," meaning "distance. That is because each of these points is four units away from Point D.

Meaning of equidistant in maths

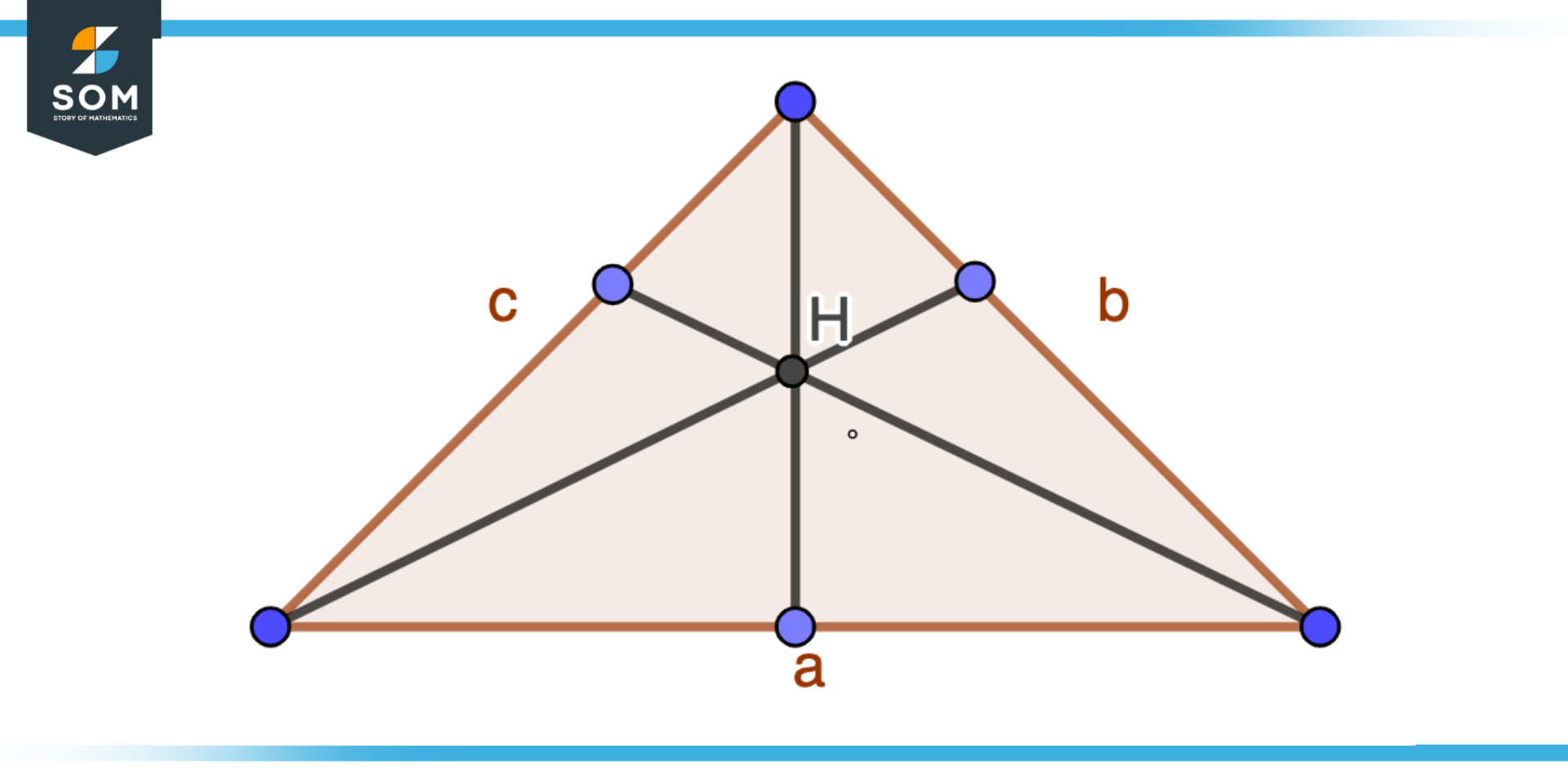
When the distances between a point and the objects in a set are equal , that point is said to be equidistant from the set. According to Euclidean geometry, the perpendicular bisector connects two points that are equidistant from each other. It follows that when two points are equidistant from two other points in three dimensions , the point is located in a plane. Suppose a scenario of a football groun d where many players have been assigned some positions as part of the lineup. Take the example of a midfielder; the midfielder position is assigned in the middle of the ground from the goal post. So we can say that the midfielder is an equidistant point that has to be in center from both the goal post. This concept is elaborated on in the above figure. Suppose another scenario where your house is located near two Apple stores. The distance from one of the apple stores to your house is 5Km and the distance from the second Apple store to your house is also 5 km , but it is not mandatory that your house will be in the middle of both stores. Your h ouse might be at perpendicular bisector of both the stores. This scenario is elaborated on in the above figure. Figure 3 — Circumcenter of Triangle Equidistant from its vertices. Typically, the circumcenter of a triangle is a point that is equally distant from each vertex. There is always a point at the c enter of a non-degenerate triangle. Likewise, cyclic polygons have equidistant circumcentres : each vertex is equally distant from its circumcentre.

Home » Introduction to Geometry » Introduction to Geometry. The center of a circle is equidistant from every point on the circle. The center of a circle is the midpoint of the diameter.

A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal. In two-dimensional Euclidean geometry , the locus of points equidistant from two given different points is their perpendicular bisector. For a triangle the circumcentre is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. This result can be generalised to cyclic polygons : the circumcentre is equidistant from each of the vertices.

Equidistant is another word for 'equally distant', which means at the same distance from a place. A point is equidistant from other points if it is at the same distance away from them. Equidistant is a term that is mostly used in geometry in the concept of parallel lines, perpendicular bisectors, circles , angle bisectors, and so on. A point is said to be equidistant from two other points when it is at an equal distance away from both of them. For example, the perpendicular bisector of a line segment is equidistant from both endpoints. Observe the following figure which shows that point Q is equidistant from P and R. There are two main formulas that are used under the topic of equidistant. We use the distance formula to find the distance between any two given points and the midpoint formula is used to find the midpoint of a line segment.

Meaning of equidistant in maths

Online Math Solver. In geometry, two or more points are said to be equidistant from each other if they are the same distance away from a third point. The term "equidistant" comes from the Latin word "aequus," which means "equal," and "distance," which comes from the Latin word "distantia," meaning "distance.

Cox communications payment address

Maths Questions. We need to know the coordinates of the two points to use the distance formula. Step 3 After naming each coordinate, the next step is to decide which formula to apply. Equidistant Definition 2. Overview Figure 1 — Midfielder Illustration for the equidistant concept Suppose a scenario of a football groun d where many players have been assigned some positions as part of the lineup. The center of a circle is the midpoint of the diameter. Point that is at the same distance to every object in a given set. The distance formula is used to find the distance between any two given points. Maths Games. Hidden categories: Articles with short description Short description matches Wikidata Articles needing additional references from August All articles needing additional references. Definition When the distances between a point and the objects in a set are equal , that point is said to be equidistant from the set.

Two or more figures that are equal in distance from each other, or equal in distance from a given point, are said to be equidistant, as in the figure below.

The distance between any two given points can be calculated by using the distance formula with the help of the coordinates of the two points. For the principle in maritime boundary claims, see Equidistance principle. Distance Formula The length of the line connecting two points is the distance between them. Equidistant means " a point which is at the same or equal distance from two given points. Home » Introduction to Geometry » Introduction to Geometry. Equidistant Definition 2. After finding the coordinates of two points and the coordinates of the midpoint next step is to give the names of each coordinate. Already booked a tutor? Find the midpoint that is equidistant from the two points. Our Journey. With Cuemath, you will learn visually and be surprised by the outcomes.