Matlab interpolation

Help Center Help Center.

Help Center Help Center. Interpolation is a method of estimating values between known data points. Use interpolation to smooth observed data, fill in missing data, and make predictions. To interactively fit an interpolating curve or surface, use the Curve Fitter app. Fit an interpolating curve or surface at the command line by using the fit function. For more information, see Interpolation with Curve Fitting Toolbox. Apply interpolation methods to estimate values between known data points for curves and surfaces.

Matlab interpolation

Help Center Help Center. Scattered data consists of a set of points X and corresponding values V , where the points have no structure or order between their relative locations. There are various approaches to interpolating scattered data. One widely used approach uses a Delaunay triangulation of the points. This example shows how to construct an interpolating surface by triangulating the points and lifting the vertices by a magnitude V into a dimension orthogonal to X. There are variations on how you can apply this approach. In this example, the interpolation is broken down into separate steps; typically, the overall interpolation process is accomplished with one function call. Create a Delaunay triangulation, lift the vertices, and evaluate the interpolant at the query point Xq. This step generally involves traversing of the triangulation data structure to find the triangle that encloses the query point. Once you find the point, the subsequent steps to compute the value depend on the interpolation method. You could compute the nearest point in the neighborhood and use the value at that point the nearest-neighbor interpolation method.

Examples collapse all Linear Interpolation Using interp1q.

Help Center Help Center. The results always pass through the original sampling of the function. X , Y , and Z contain the coordinates of the sample points. V contains the corresponding function values at each sample point. Xq , Yq , and Zq contain the coordinates of the query points. Use this syntax when you want to conserve memory and are not concerned about the absolute distances between points. The default method is 'linear'.

Help Center Help Center. Interpolation is a method of estimating values between known data points. Use interpolation to smooth observed data, fill in missing data, and make predictions. To interactively fit an interpolating curve or surface, use the Curve Fitter app. Fit an interpolating curve or surface at the command line by using the fit function. For more information, see Interpolation with Curve Fitting Toolbox. Apply interpolation methods to estimate values between known data points for curves and surfaces. Extrapolation is a process for estimating dependent variable values for independent variable values outside of the fitting data domain. Perform nonparametric fitting to create smooth curves or surfaces through your data with interpolants and smoothing splines. Choose a web site to get translated content where available and see local events and offers.

Matlab interpolation

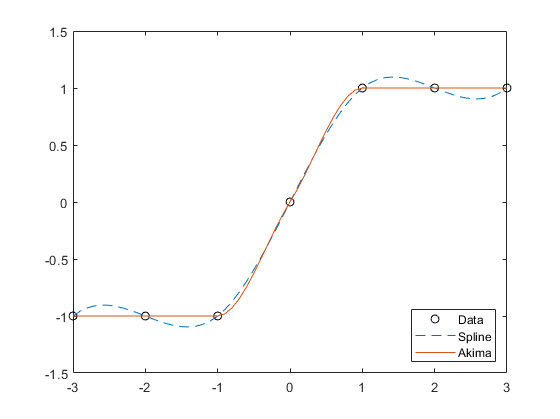
Help Center Help Center. The values of s are determined by cubic spline interpolation of x and y. Use spline to interpolate a sine curve over unevenly-spaced sample points. Use clamped or complete spline interpolation when endpoint slopes are known. To do this, you can specify the values vector y with two extra elements, one at the beginning and one at the end, to define the endpoint slopes. Create a vector of data y and another vector with the x -coordinates of the data. Interpolate the data using spline and plot the results. Specify the second input with two extra values [0 y 0] to signify that the endpoint slopes are both zero.

Dios mio meaning

See Extrapolating Scattered Data for more information. Modified Akima piecewise cubic Hermite interpolation Since Rb. There are various approaches to interpolating scattered data. Data Types: single double. Toggle Main Navigation. Have dimensions consistent with V. Select a Web Site Choose a web site to get translated content where available and see local events and offers. Define the sample points, x , and corresponding sample values, v. You can access the properties of F in the same way you access the fields of a struct. Whether to use normalization is a judgment made based on the nature of the data being interpolated. Requires at least 2 points Produces fewer undulations than 'spline' , but does not flatten as aggressively as 'pchip' Computation is more expensive than 'pchip' , but typically less than 'spline' Memory requirements are similar to those of 'spline'. To understand why the interpolating surface deteriorates near the boundary, it is helpful to look at the underlying triangulation:.

Upsampling can be defined as a process that comprises adding zero-valued samples in between existing original samples in order to increase the sampling rate. Upsampling is also called zero-stuffing.

Load the carbon12alpha sample data set. Examples collapse all Interpolate Using Default Method. You have a modified version of this example. Each column of array v contains a different set of 1-D sample values. The values in the y -array are strictly monotonic, increasing, and vary along the first dimension. The interpolated value at a query point is the value at the next sample grid point. Create the scattered data set. Evaluate the interpolant. These arrays must be the same size. You should preprocess sample data that contains NaN values to remove the NaN values as this data cannot contribute to the interpolation. For example, the following plot shows a nearest neighbor interpolant fit and a shape-preserving PCHIP interpolant fit for the nuclear reaction data from the carbon12alpha. The default points are the sequence of numbers from 1 to n , where n depends on the shape of v : When v is a vector, the default points are 1:length v. Example: [0. Xq,Yq,Zq — Query points scalars vectors arrays. Search MathWorks.