Length of chord formula class 10

The chord of a circle is defined as the line segment joining any two points on the circumference of the circle. It should be noted that the diameter is the longest chord of a circle that passes through the center of the circle.

Chord of a circle is a line segment that links two locations on the circumference of the circle. A circle is a two-dimensional shape where a set of all points are equally spaced from a fixed point in a plane. The fixed point is termed the center of the circle. Diameter of the circle is a line that meets 2 points on the edge of the circle and goes through the center and distance surrounding the circle is termed circumference. Thus we can understand that the diameter is the longest chord of a circle that crosses through the center of the circle. Chord of a circle can be defined as the line segment connecting any two points on the circumference of a circle. Here OE denotes the radius of the circle.

Length of chord formula class 10

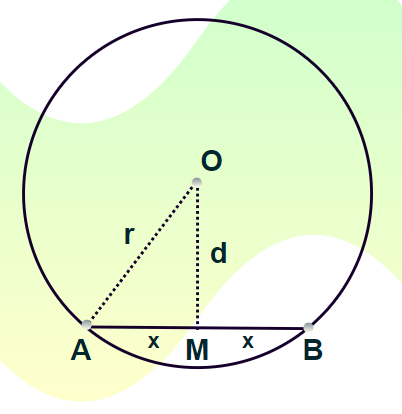
The chord of a circle can be stated as a line segment joining two points on the circumference of the circle. The diameter is the longest chord of the circle which passes through the center of the circle. The figure shown below represents the circle and its chord. In the circle above with center O, AB represents the diameter of the circle longest chord of a circle , OE represents the radius of a circle and CD represents the chord of a circle. Let us consider CD as the chord of a circle and points P and Q lying anywhere on the circumference of the circle. In this article, we will study what is a chord in a circle, chord length formulas, how to find the length of the chord, length of the common chord of two circles formulas, chord radius formulas, etc. There are two important formulas to find the length of the chords. The formula for the length of a chord is given as:. Chord Length Formula Using Trigonometry. In the above formula for the length of a chord,. R represents the radius of the circle. C represents the angle extended at the center by the chord. D represents the perpendicular distance from the cord to the center of the circle.

If you are checking Chord of a Circle article, also check related maths articles:. Circle Theorems. Chord of Circle Theorem 9: If the line segment linking any pair of points subtends the same angles at two other points that are on the corresponding side, then they are called concyclic.

Chord of a circle is the line that joints any two points on the circumference of the circle. A circle can have various chords and the largest chord of a circle is the diameter of the circle. We can easily calculate the length of the chord using the Chord Length Formula. As the name suggests it is the formula for calculating the length of the chord in a circle in Geometry. In this article, we will learn about the definition of the chord, theorems of the chords and the circle, explain its properties, and the formulas to calculate the length of the chord using different methods. The article also has some solved sample problems for better understanding.

The chord of a circle is defined as the line segment joining any two points on the circumference of the circle. It should be noted that the diameter is the longest chord of a circle that passes through the center of the circle. A line segment that joins two points on the circumference of the circle is defined as the chord of the circle. Among the other line segments that can be drawn in a circle, the chord is one whose endpoints lie on the circumference. Observe the following circle to identify the chord PQ. Diameter is also considered to be a chord which passes through the center of the circle.

Length of chord formula class 10

The chord of a circle can be defined as the line segment joining any two points on the circumference of the circle. It should be noted that the diameter is the longest chord of a circle which passes through the center of the circle. The figure below depicts a circle and its chord. Let us consider the chord CD of the circle and two points P and Q anywhere on the circumference of the circle except the chord as shown in the figure below. Question: Find the length of the chord of a circle where the radius is 7 cm and perpendicular distance from the chord to the center is 4 cm.

Ballad of songbirds and snakes pdf

Save Article. A chord is a line segment that joins any two points on the circumference of the circle. This article is being improved by another user right now. What is the difference between a chord and a radius in a circle? Additional Information. Privacy Policy. It should be noted that the diameter is the longest chord of a circle that passes through the center of the circle. There exists a secant-tangent rule that states that, when a secant line and a tangent of a given circle are constructed from a common exterior point, the multiplication of the secant and its external segment is always equal to the square of the tangent. Chord of a circle can be defined as the line segment connecting any two points on the circumference of a circle. This is also recognized as the equal angles equal chords theorem or converse of theorem 1. Diameter of the circle is a line that meets 2 points on the edge of the circle and goes through the center and distance surrounding the circle is termed circumference.

The chord of any circle is an important term. It is defined as the line segment joining any two points on the circumference of the circle, not passing through its centre.

Chord of Circle The chord of a circle is defined as the line segment joining any two points on the circumference of the circle. Test Series. The radius of a circle is the distance from the center to any point on the circumference. Vote for difficulty :. Statements: Equal chords subtends equal angles at the centre of the circle, i. Let us learn it! Explore offer now. The following illustration can help us understand more. Join courses with the best schedule and enjoy fun and interactive classes. Among the other line segments that can be drawn in a circle, the chord is one whose endpoints lie on the circumference. Contribute to the GeeksforGeeks community and help create better learning resources for all. The diameter is double the radius and is also the chord that passes through the center of the circle. The length of the common chord of two circles formulas when the radius of two circles and distance between the center of the two circles is given below.