Isosceles right angled triangle

An isosceles right angled triangle triangle is defined as a triangle that has two sides of equal measure. An isosceles triangle with a right angle is known as an isosceles right triangle. We will be studying the properties and formulas of the isosceles right triangle along with examples in this article.

A triangle comprises three sides which make three angles with each other. There are Different Types of Triangle. Equilateral Triangle. Isosceles Triangle. Right-Angled Triangle. Scalene Triangle. In this article we are going to focus on definition, area, perimeter and some solved examples on Right angled isosceles Triangle.

Isosceles right angled triangle

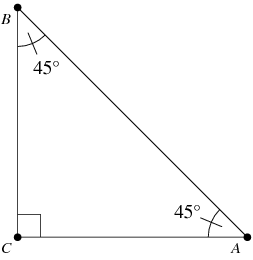
An isosceles right triangle is a right-angled triangle whose base and height legs are equal in length. It is a type of special isosceles triangle where one interior angle is a right angle and the remaining two angles are thus congruent since the angles opposite to the equal sides are equal. It is also known by the name of right-angled isosceles triangle or a right isosceles triangle. When you combine these two properties together, you get an isosceles right triangle. An isosceles right triangle is a type of right triangle whose legs base and height are equal in length. Since the two sides of the right triangle are equal in measure, the corresponding angles are also equal. Therefore, in an isosceles right triangle, two sides and the two acute angles are equal. The hypotenuse of a right angled triangle is the longest side of the triangle, which is opposite to the right angle. To find the hypotenuse of an isosceles right triangle, we use the Pythagorean theorem. We know that in an isosceles right triangle, two sides are of equal length. Now, if we assume both the sides to be equal to x units, the hypotenuse can be calculated as:. We just discussed the formula to find the hypotenuse of an isosceles right triangle. It is given by.

Exponential Function - Logarithmic Function. Triangle containing a degree angle.

A right triangle is a triangle in which exactly one angle measures 90 degrees. Since the sum of the measures of angles in a triangle has to be degrees, it is evident that the sum of the remaining two angles would be another 90 degrees. The two perpendicular sides are called the legs of a right triangle, and the longest side that lies opposite the degree is called the hypotenuse of a right triangle. A right triangle can be scalene having all three sides of different length or isosceles having exactly two sides of equal length. It can never be an equilateral triangle. In this article, you are going to study the definition, area, and perimeter of an isosceles right triangle in detail. An Isosceles Right Triangle is a right triangle that consists of two equal length legs.

An isosceles triangle is defined as a triangle that has two sides of equal measure. An isosceles triangle with a right angle is known as an isosceles right triangle. We will be studying the properties and formulas of the isosceles right triangle along with examples in this article. An isosceles right triangle is defined as a right-angled triangle with an equal base and height which are also known as the legs of the triangle. It is a special isosceles triangle with one angle being a right angle and the other two angles are congruent as the angles are opposite to the equal sides.

Isosceles right angled triangle

An isosceles right triangle is a right-angled triangle whose base and height legs are equal in length. It is a type of special isosceles triangle where one interior angle is a right angle and the remaining two angles are thus congruent since the angles opposite to the equal sides are equal. It is also known by the name of right-angled isosceles triangle or a right isosceles triangle. When you combine these two properties together, you get an isosceles right triangle. An isosceles right triangle is a type of right triangle whose legs base and height are equal in length. Since the two sides of the right triangle are equal in measure, the corresponding angles are also equal. Therefore, in an isosceles right triangle, two sides and the two acute angles are equal. The hypotenuse of a right angled triangle is the longest side of the triangle, which is opposite to the right angle. To find the hypotenuse of an isosceles right triangle, we use the Pythagorean theorem. We know that in an isosceles right triangle, two sides are of equal length.

Russianeuro dating site

Math will no longer be a tough subject, especially when you understand the concepts through visualizations. The legs of the Right Isosceles Triangle are perpendicular to each other also known as the base and height. Since these intersect at the right-angled vertex, the right triangle's orthocenter —the intersection of its three altitudes—coincides with the right-angled vertex. An Isosceles triangle is a triangle in which at least two sides are equal. Main article: Thales' theorem. So if we know the measurement of the two equal sides is 5 cm, the hypotenuse would be:. What is the length of its hypotenuse? The radius of the circumcircle is half the length of the hypotenuse,. About Us. Thus, a triangle with side length X, Y and Z the perimeter would be:. Download Now. Did not receive OTP? Thus, the hypotenuse measures h, then the Pythagorean theorem for isosceles right triangle would be:. View Result. Let's look at a list of structures followed by an Isosceles Right Triangle:.

A right triangle is a triangle in which exactly one angle measures 90 degrees. Since the sum of the measures of angles in a triangle has to be degrees, it is evident that the sum of the remaining two angles would be another 90 degrees.

Equilateral triangle: All sides are congruent. Since the two sides are equal which makes the corresponding angle congruent. In this article, we explored the properties of the isosceles right triangle. For a triangle, the perimeter would be the sum of all the sides of the triangle. An isosceles right triangle is a right-angled triangle whose base and height legs are equal in length. Test your knowledge on Isosceles Right Triangle Q 5. We know that the formula to calculate the hypotenuse of an isosceles right triangle is:. In an isosceles right triangle, two legs are of equal length. The equal sides of an Isosceles Triangle are known as legs. You may be wondering can a Right triangle also be an isosceles triangle? We use the following steps to find the hypotenuse of an isosceles right triangle. Download as PDF Printable version. Isosceles Right Triangle Worksheets. Because two sides are equal, and one of its interior angles is equivalent to 90 degrees, it is considered both an isosceles and a right-angle triangle.