Integral of sinx
Integral of sinx along with its formula and proof with examples. Also learn how to calculate integration of sinx with step by step examples. In calculusthe integral is a fundamental concept that assigns numbers to functions to define displacement, integral of sinx, area, volume, and all those functions that contain a combination of tiny elements.
Today we have a tough integral: not only is this a special integral the sine integral Si x but it also goes from 0 to infinity! We need to use a different approach: differentiation under the integral sign also known as Feynman technique. The idea is that we introduce a parameter so that, when differentiating with respect to the parameter a certain function that contains it, something happens that will make the integral easier to evaluate. In this case, in order to make this integral easy, we need to get rid of that x at the denomitator; to do so we need to differentiate a function that contains a parameter multiplied by x so that the x is generated and the one at the denominator will cancel out with it. This means this is not the right way to go.
Integral of sinx
Integral Calculus is the process of summing up small parts of something into one. In mathematics, it is the process of doing the sum total of functions. There are so many functions in mathematics that can be integrated. Trigonometric functions too can be integrated. In this article, we will study the integral of sin x dx, its formula, derivation with proof, graph along with some solved examples. At the simplest level, integration is the process of combining two or more things to create a whole. When you integrate some function f x , you find its antiderivative function, which is often denoted F x. Tan is a trigonometric function that relates the two sides of a right-angled triangle to an angle. The Sine is a trigonometrical ratio of the adjacent sides and hypotenuse. Continue reading about second order derivatives. Write the derivative of the cos function with respect to x formula for expressing the differentiation of the cosine function in mathematical form.
Now the integration becomes. Is it something I did? Since integral is nothing but anti-derivative, integral of sinx, the integral of sin x is -cos x of course, we add the integration constant C to this.
Your options:. Describing an integral as "area under the curve" is like describing a book as a list of words. Technically correct, but misses the message and I suspect you haven't done the assigned reading. The integral is just fancy multiplication. But if we squint our eyes and pretend items are identical we have a multiplication. Yes, it's also fancy curve with nice properties. Just regular numbers.
In this section we look at how to integrate a variety of products of trigonometric functions. These integrals are called trigonometric integrals. They are an important part of the integration technique called trigonometric substitution , which is featured in Trigonometric Substitution. This technique allows us to convert algebraic expressions that we may not be able to integrate into expressions involving trigonometric functions, which we may be able to integrate using the techniques described in this section. In addition, these types of integrals appear frequently when we study polar, cylindrical, and spherical coordinate systems later. For integrals of this type, the identities.
Integral of sinx
Wolfram Alpha is a great tool for calculating antiderivatives and definite integrals, double and triple integrals, and improper integrals. The Wolfram Alpha Integral Calculator also shows plots, alternate forms and other relevant information to enhance your mathematical intuition. Use Math Input above or enter your integral calculator queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for an integral using plain English. Get immediate feedback and guidance with step-by-step solutions for integrals and Wolfram Problem Generator. The indefinite integral of , denoted , is defined to be the antiderivative of. In other words, the derivative of is.
Lion king coloring
Don't let team Integrals Are Literal Area win every battle! We need to use a different approach: differentiation under the integral sign also known as Feynman technique. Or just a quantity helplessly shrinking? Related Problems. What Is Integration of Sinx? To calculate these areas approximately, we drew the triangles. Integral of Sin x Proof by Derivatives. Let us make it what we wanted by multiplying both sides by Before going to find the integral of sin x, let us recall what is integral. It means that the derivative of cos x gives us sin x. Alan Walker- Published on To find the Integral of sinx we use the integration by substitution method. With those 3 intuitions, our rough rough! With awkward negatives to swap the axes.
Functions involving trigonometric functions are useful as they are good at describing periodic behavior. This section describes several techniques for finding antiderivatives of certain combinations of trigonometric functions.
This puts us at a new position. To find the Integral of sinx we use the integration by substitution method. Maths Puzzles. Then the above equation becomes,. Important Links. Don't let team Integrals Are Literal Area win every battle! We know that integration is the reverse process of differentiation. By similar triangles, our change just just our original triangle, rotated and scaled. Integral of Sin x Proof by Substitution Method. An integral is also known as the antiderivative. Appendix: Height controls width? What is the integral of sin? Stay up to date with the latest integration calculators, books, integral problems, and other study resources. Your options: Pretend to be asleep except not in the engineering library again Canned response: "As with any function, the integral of sine is the area under its curve. Therefore, to obtain the integral of sine, we have to multiply the above equation by a negative sign, that is:.

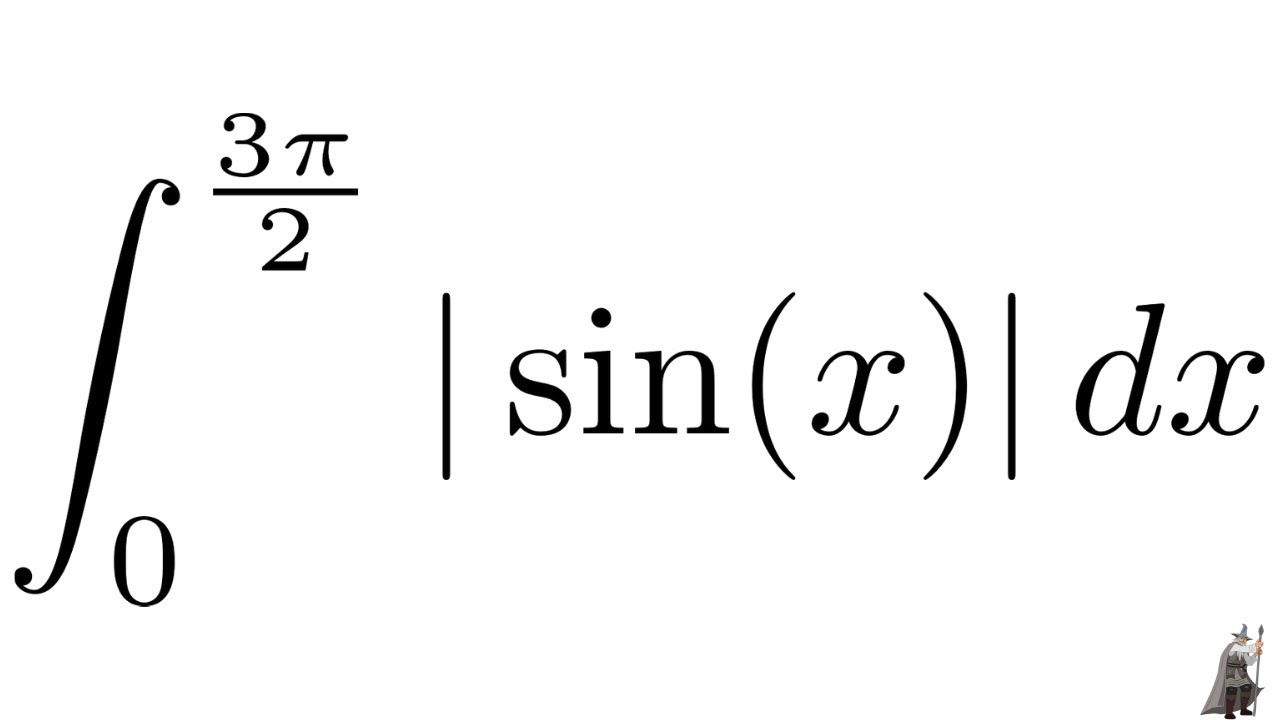
You have hit the mark. In it something is also to me it seems it is good idea. I agree with you.