Integral 1 sqrt x 2 a 2
When this page was first created back in the late s, it was nearly impossible to locate tables of integrals both definite and indefinite on the Internet.
This can be done using various substitutions. We will look at a hyperbolic substitution at the end of this page. It can also be done using the substitution. But that is begging the question because it feels like we have to know the answer to come up with that idea. We could also do the substitution. The above can be found in various sources, so we will not go through that here, but instead, we will find the answer to our integral using simple complex analysis.
Integral 1 sqrt x 2 a 2
.
We may start by noting that and thus that If z is larger than one the logarithm is not negative, since and we can also see that this function is increasing, but less and less fast. So we get. Let us first pull out a factor of -1 from the square root, and then the rule from the previous page, to get.
.
This calculator computes the definite and indefinite integrals antiderivative of a function with respect to a variable x. Supported functions: sqrt, ln use 'ln' instead of 'log' , e use 'e' instead of 'exp'. Welcome to MathPortal. I designed this website and wrote all the calculators, lessons, and formulas. If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected].
Integral 1 sqrt x 2 a 2
Antiderivative calculator finds the antiderivative of a function step by step with respect to a variable i. This online integration calculator also supports upper bound and lower bound in case you are working with minimum or maximum value of intervals. It can find the integrals of logarithmic as well as trigonometric functions. This tool assesses the input function and uses integral rules accordingly to evaluate the integrals for the area, volume, etc. You can find the antiderivative integral of any function by following the steps below. An integral can be defined as,. The process of finding integrals is called integration. Integral is also referred to as antiderivative because it is a reverse operation of derivation.
Togc mount
We may start by noting that and thus that If z is larger than one the logarithm is not negative, since and we can also see that this function is increasing, but less and less fast. So we get For symmetry reasons we also have as shown in the graph below. Copyright - All trademarks, copyrights, patents, and other rights of ownership to images and text used on the RF Cafe website are hereby acknowledged. It can also be done using the substitution But that is begging the question because it feels like we have to know the answer to come up with that idea. We put the constant of integration back later on. The above can be found in various sources, so we will not go through that here, but instead, we will find the answer to our integral using simple complex analysis. Kirt Blatten berger ,. We could also do the substitution But that will require us to know or figure out, that which is quite easy to find. You can get it from in a couple of steps. The function should be the derivative of the above logarithmic expression. So this means that. Using complex analysis We will use complex analysis, or rather just complex numbers and a bit of calculus in a rather straightforward way. The World Wide Web Internet was largely an unknown entity at the time and bandwidth was a scarce commodity.
.
You can find more on those here. Technically we are done, but it is in a not all too useful form. Let us first pull out a factor of -1 from the square root, and then the rule from the previous page, to get. Here we let the constant absorb the ln i. Copyright - All trademarks, copyrights, patents, and other rights of ownership to images and text used on the RF Cafe website are hereby acknowledged. From a previous section , we have that. Let us first pull out a factor of -1 from the square root, and then the rule from the previous page, to get Technically we are done, but it is in a not all too useful form. The process of solving for antiderivatives is antidifferentiation or indefinite integration. We may start by noting that and thus that If z is larger than one the logarithm is not negative, since and we can also see that this function is increasing, but less and less fast. Next comes the question of which sign to use. In calculus, an antiderivative, primitive, or indefinite integral of a function f is a function F whose derivative is equal to f, i.

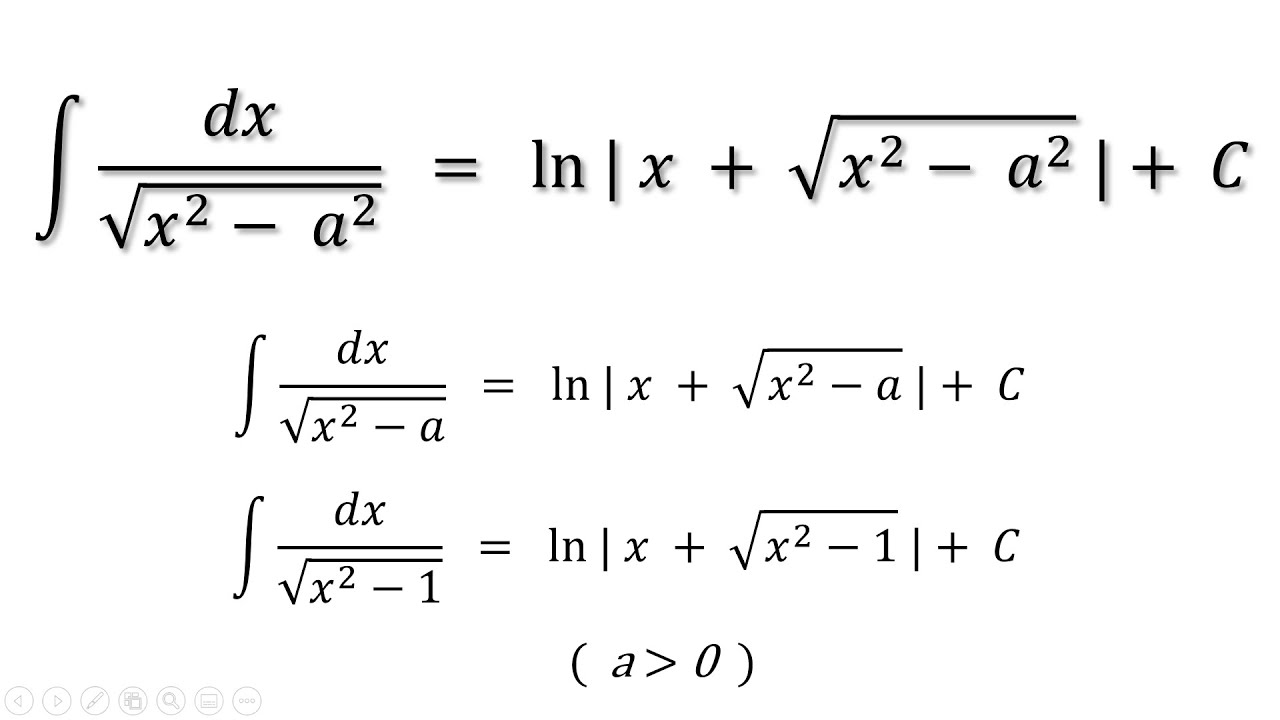
I congratulate, what excellent answer.
Talently...