How to find oblique asymptotes using limits
We have shown how to use the first and second derivatives of a function to describe the shape of a graph. In this section, we define limits at infinity and show how these limits affect the graph of a function.
We use MathJax. Many functions exhibit asymptotic behavior. Graphically, that is to say that their graph approaches some other geometric object usually a line as the graph of the function heads away from the area around the origin. In other words, asymptotic behavior involves limits, since limits are how we mathematically describe situations where a function approaches a value. In college algebra, you may have learned how to locate several type of asymptotes.
How to find oblique asymptotes using limits
.
We start by graphing a polynomial function. We can extend this idea to limits at infinity. A function is not limited in the number of vertical asymptotes it may have.
.
In my experience, students often hit a roadblock when they see the word asymptote. What is an asymptote anyway? How do you find them? Is this going to be on the test??? The answer to the last question is yes. Asymptotes definitely show up on the AP Calculus exams. Of the three varieties of asymptote — horizontal , vertical , and oblique — perhaps the oblique asymptotes are the most mysterious.
How to find oblique asymptotes using limits
We have shown how to use the first and second derivatives of a function to describe the shape of a graph. In this section, we define limits at infinity and show how these limits affect the graph of a function. We begin by examining what it means for a function to have a finite limit at infinity.
We don t talk anymore lyrics in english
Go back to previous article. What is really required to justify this statement is either the Sandwich Theorem or a delta-epsilon proof or actually, an M-epsilon proof. If a rational function has an oblique linear asymptote, it can be found by division. First, using long division of polynomials, we can write. Solution a. In college algebra, you may have learned how to locate several type of asymptotes. We have shown how to use the first and second derivatives of a function to describe the shape of a graph. In fact, a function may cross a horizontal asymptote an unlimited number of times. The end-behavior function should meet the same asymptotic requirement that we have used for lines. When doing so, we see that. The end behavior for rational functions and functions involving radicals is a little more complicated than for polynomials. Since there is only one solution, there can be at most one vertical asymptote. Then we study the idea of a function with an infinite limit at infinity. We then look at how to use these definitions to prove results involving limits at infinity. Although these terms provide accurate descriptions of limits at infinity, they are not precise mathematically.
We use MathJax. Many functions exhibit asymptotic behavior.
In college algebra, you may have learned how to locate several type of asymptotes. A function can have at most two horizontal asymptotes, one in each direction. To find the oblique asymptote, use long division of polynomials to write. Formal Definitions Earlier, we used the terms arbitrarily close, arbitrarily large, and sufficiently large to define limits at infinity informally. For rational functions, the end-behavior candidate is typically found by dividing. This is another handwaving argument, as we had in the previous example, and it also really requires either the Sandwich Theorem or a delta-epsilon proof. Then we study the idea of a function with an infinite limit at infinity. Consider a rational function. Recognize a horizontal asymptote on the graph of a function. First, using long division of polynomials, we can write.

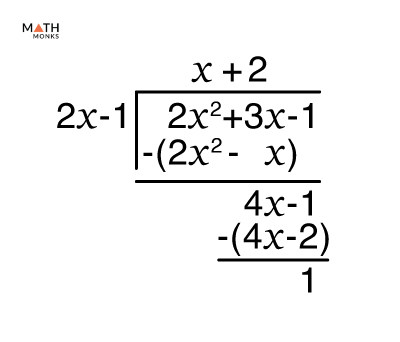
Completely I share your opinion. It seems to me it is excellent idea. I agree with you.
Certainly. And I have faced it. Let's discuss this question.
I am sorry, that has interfered... I here recently. But this theme is very close to me. I can help with the answer. Write in PM.