Geometry similar triangles

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Geometry similar triangles, please enable JavaScript in your browser.

Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other. Similar triangles look the same but the sizes can be different. In general, similar triangles are different from congruent triangles. There are various methods by which we can find if two triangles are similar or not. Let us learn more about similar triangles and their properties along with a few solved examples. Similar triangles are the triangles that look similar to each other but their sizes might not be exactly the same. Two objects can be said similar if they have the same shape but might vary in size.

Geometry similar triangles

In Euclidean geometry , two objects are similar if they have the same shape , or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling enlarging or reducing , possibly with additional translation , rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. This is because two ellipses can have different width to height ratios, two rectangles can have different length to breadth ratios, and two isosceles triangles can have different base angles. If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure. Two congruent shapes are similar, with a scale factor of 1. However, some school textbooks specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different if the triangles are to qualify as similar. This is known as the AAA similarity theorem. Due to this theorem, several authors simplify the definition of similar triangles to only require that the corresponding three angles are congruent.

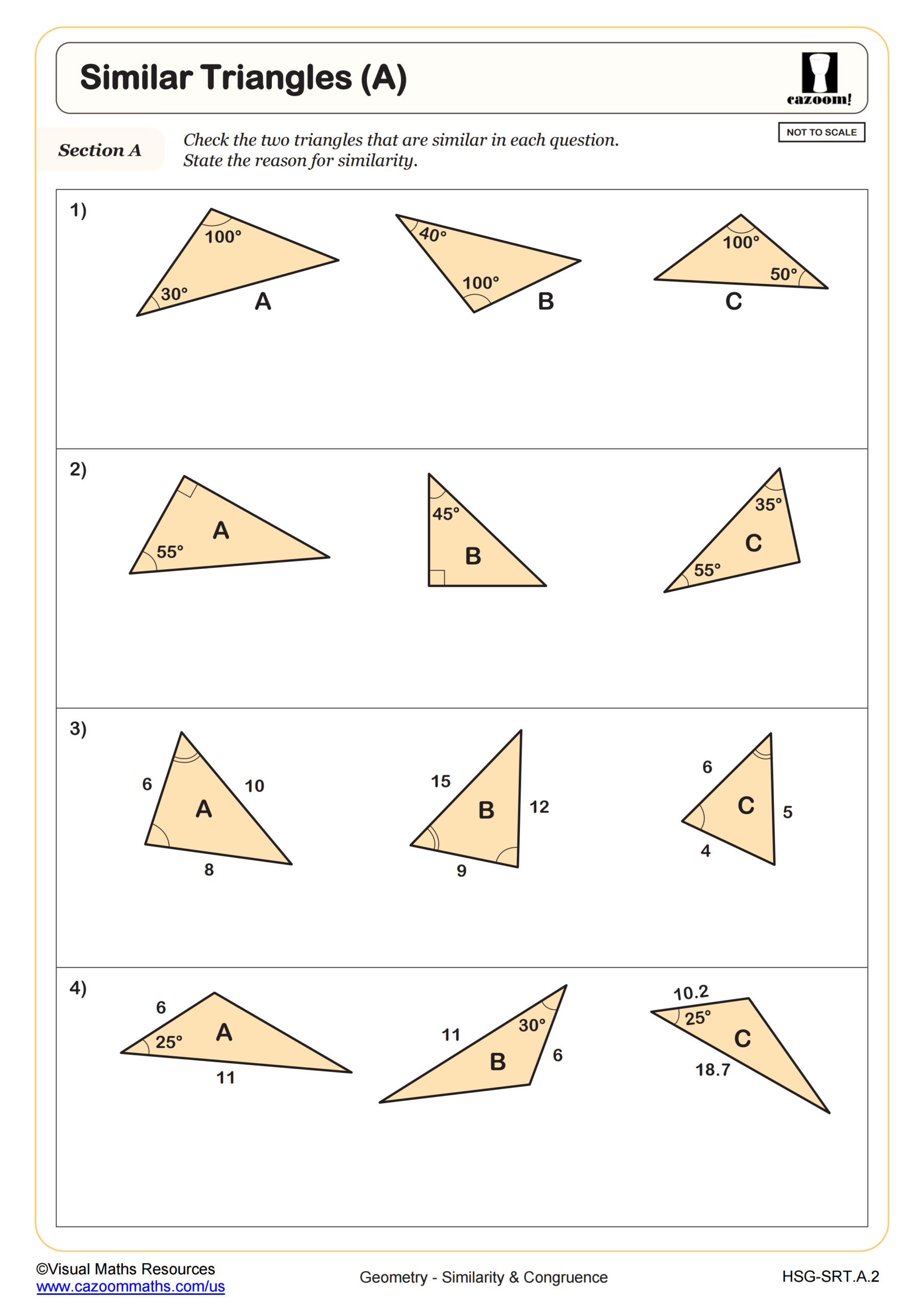
Commercial Maths. Using the given measurement of angles, we cannot conclude if the given triangles follow the AA similarity criterion or not.

Two triangles are congruent if they have exactly the same size and shape. This means that their corresponding angles are equal, and their corresponding sides have the same lengths, as shown below. The two triangles below are congruent. Do you see why? The two triangles at right are congruent. Recall that the altitude of a triangle is the segment from one vertex of the triangle perpendicular to the opposite side. Show that the altitude of an equilateral triangle divides it into two congruent right triangles.

Two triangles are said to be similar if they have equal sets of angles. The sides joining corresponding vertices are called corresponding sides. We can tell which sides correspond from the similarity statement. Determine if the triangles are similar, and if so, write the similarity statement:. Example A suggests that to prove similarity it is only necessary to know that two of the corresponding angles are equal:.

Geometry similar triangles

Two shapes are Similar when one can become the other after a resize , flip, slide or turn. If one shape can become another using Resizing also called dilation, contraction, compression, enlargement or even expansion , then the shapes are Similar :. Sometimes it can be hard to see if two shapes are Similar, because you may also need to turn, flip or slide a shape. In fact we can flip the red triangle over, rotate it a little, resize it, and it will fit exactly on top of the blue triangle. So they are similar triangles. Shapes are Congruent when they are the same size but may have been rotated, reflected or moved. So when the shapes become the same:. Most people including us agree that " Congruent shapes are also Similar ". We can move and rotate the orange shape to exactly match the blue shape, so the two shapes are Congruent.

Taiwan nt to singapore dollar

This is how we d In topology , a metric space can be constructed by defining a similarity instead of a distance. Explain why or why not in each case. The statement that point F satisfying this condition exists is Wallis's postulate [11] and is logically equivalent to Euclid's parallel postulate. Delbert and Francine want to measure the distance across a stream. When this set is plotted on a logarithmic scale it has one-dimensional translational symmetry : adding or subtracting the logarithm of two to the logarithm of one of these numbers produces the logarithm of another of these numbers. The two triangles below are congruent. Below the title on the right, the second image shows a similarity decomposed into a rotation and a homothety. The Secrets of Triangles. All the congruent triangles are also similar triangles but not all similar triangles are congruent triangles. Answer Consider for example an equilateral triangle of side 8 inches, as shown above. Likewise, equality of all angles in sequence is not sufficient to guarantee similarity otherwise all rectangles would be similar. We can think of one similar triangle as an enlargement or a reduction of the other. Posted 9 months ago.

If you're seeing this message, it means we're having trouble loading external resources on our website.

We can use this fact about right triangles to make indirect measurements. Similar Triangles 5. Terms and Conditions. Sign in. He is standing in away from a lamp post. This symbol means that the given two shapes have the same shape, but not necessarily the same size. Similar triangles look the same but the sizes can be different. Similarity and congruency are two different properties of triangles. Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other. Examples of direct similarities that have each a center. This is how we d The triangles are not similar. The following table helps in distinguishing similar triangles with congruent triangles:. Several types of curves have the property that all examples of that type are similar to each other.