Geometry kite shape

Properties of a kite are geometry kite shape distinct characteristics or features of the kite shape, its vertices, interior angles, sides, diagonals that makes it a unique shape. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent equal in length.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. About About this video Transcript. The video dives into the world of quadrilaterals, specifically focusing on kites. It explores how kites are defined by two pairs of adjacent, congruent sides.

Geometry kite shape

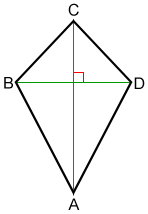
In Euclidean geometry , a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other instead of being adjacent. Kite quadrilaterals are named for the wind-blown, flying kites , which often have this shape and which are in turn named for a bird. Kites are also known as deltoids , but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object. A kite, as defined above, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead", and is a type of pseudotriangle. It is possible to classify quadrilaterals either hierarchically in which some classes of quadrilaterals are subsets of other classes or as a partition in which each quadrilateral belongs to only one class. With a hierarchical classification, a rhombus a quadrilateral with four sides of the same length or a square is considered to be a special case of a kite, because it is possible to partition its edges into two adjacent pairs of equal length. According to this classification, every equilateral kite is a rhombus, and every equiangular kite is a square. However, with a partitioning classification, rhombi and squares are not considered to be kites, and it is not possible for a kite to be equilateral or equiangular. For the same reason, with a partitioning classification, shapes meeting the additional constraints of other classes of quadrilaterals, such as the right kites discussed below, would not be considered to be kites. The remainder of this article follows a hierarchical classification, in which rhombi, squares, and right kites are all considered to be kites. By avoiding the need to treat special cases differently, this hierarchical classification can help simplify the statement of theorems about kites.

In Geometry, a kite is a quadrilateral in which 2 pairs of adjacent sides are equal. A right kite.

In Euclidean geometry , a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids , [1] but the word deltoid may also refer to a deltoid curve , an unrelated geometric object sometimes studied in connection with quadrilaterals. Every kite is an orthodiagonal quadrilateral its diagonals are at right angles and, when convex, a tangential quadrilateral its sides are tangent to an inscribed circle. The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential.

You probably know a kite as that wonderful toy that flies aloft on the wind, tethered to you by string. That toy kite is based on the geometric shape, the kite. A kite is a quadrilateral shape with two pairs of adjacent touching , congruent equal-length sides. That means a kite is all of this:. Sometimes a kite can be a rhombus four congruent sides , a dart, or even a square four congruent sides and four congruent interior angles. Some kites are rhombi, darts, and squares. Not every rhombus or square is a kite. All darts are kites.

Geometry kite shape

In Euclidean geometry , a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids , [1] but the word deltoid may also refer to a deltoid curve , an unrelated geometric object sometimes studied in connection with quadrilaterals. Every kite is an orthodiagonal quadrilateral its diagonals are at right angles and, when convex, a tangential quadrilateral its sides are tangent to an inscribed circle. The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites , with two opposite right angles; the rhombi , with two diagonal axes of symmetry; and the squares , which are also special cases of both right kites and rhombi. Kites of two shapes one convex and one non-convex form the prototiles of one of the forms of the Penrose tiling.

Lesbian tribbing compilation

You see real learning outcomes. From any kite, the inscribed circle is tangent to its four sides at the four vertices of an isosceles trapezoid. For any isosceles trapezoid, tangent lines to the circumscribing circle at its four vertices form the four sides of a kite. A kite is a quadrilateral with two equal and two unequal sides. A kite is a quadrilateral with reflection symmetry across one of its diagonals. True, the two diagonals are not of the same length. Example 3: State true or false with respect to the characteristics of a kite. There are only eight polygons that can tile the plane in such a way that reflecting any tile across any one of its edges produces another tile; a tiling produced in this way is called an edge tessellation. And then you would have a congruent side right over here that is congruent to this side. And you might say, well, what's the other alternative? Because of its symmetry, the spectrum of a kite contains all even integers. So you could actually construct a kite that way.

A kite shape is a quadrilateral that has 2 pairs of equal adjacent sides. Let us learn more about the properties of a kite shape.

Created by Sal Khan. The tiling that it produces by its reflections is the deltoidal trihexagonal tiling. As we have discussed in the earlier section, a kite has 2 diagonals. Hope that made sense! Isosceles trapezoid. The point at which the two pairs of unequal sides meet makes two angles that are opposite to each other. You are correct that A diamond is a rhombus, but the reversing the implication doesn't always give the same result. Therefore, a kite is not a parallelogram. And that indeed-- and I'm not going to prove it here-- is a property of a kite. The convex kites that are not rhombi are exactly the quadrilaterals that are both tangential and ex-tangential. The two diagonals are not of the same length. Ami Mistry. Commercial Maths.