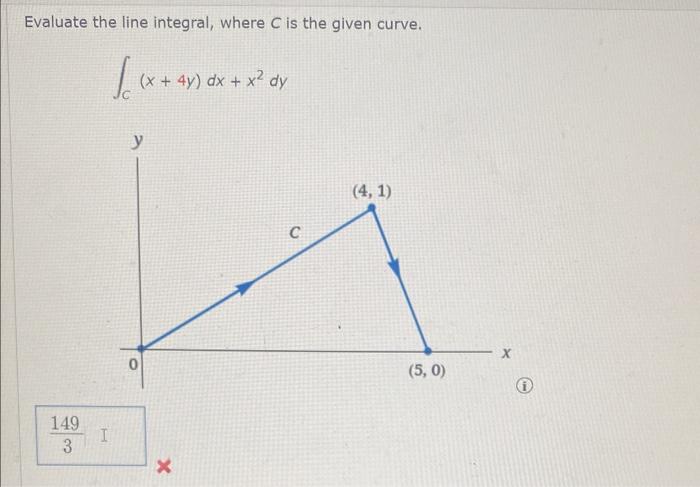
Evaluate the line integral where c is the given curve

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a0 a0 and b0 b0 —in other words, a line segment located on the x -axis. Suppose we want to integrate over any curve in the plane, not just over a line segment on the x -axis. Such a task requires a new kind of integral, called a line integral.

In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve. A line integral is also called the path integral or a curve integral or a curvilinear integral. In this article, we are going to discuss the definition of the line integral, formulas, examples, and the application of line integrals in real life. A line integral is integral in which the function to be integrated is determined along a curve in the coordinate system. The function which is to be integrated may be either a scalar field or a vector field. We can integrate a scalar-valued function or vector-valued function along a curve. The value of the line integral can be evaluated by adding all the values of points on the vector field.

Evaluate the line integral where c is the given curve

Q: Evaluate the line integral, where C is the given curve. Q: evaluate the line integral along the curve C. Q: Find the line integral of x ds over C where c is the line segment from 1,0 to 0,1 using two…. A: Given. A: Line integral. Q: Evaluate the line integral, where C is the given cu curve. A: C consist line from A 2, 0, 1 to B 3, 3, 1 Now,. A: Find the equation of line in parametric form. C: x-axis from 0, 0 to 0, -3 …. Q: Evaluate the line integral along the given paths. A: We need to evaluate,. For a ,. A: Note:-Our guidelines we are supposed to answer only one question. Kindly repost other question as…. A: Explained below.

Similar questions. Scalar line integrals have many applications.

We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals. We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals''. As with other integrals, a geometric example may be easiest to understand. What is the area of the surface thus formed? We already know one way to compute surface area, but here we take a different approach that is more useful for the problems to come. As usual, we start by thinking about how to approximate the area. We pick some points along the part of the parabola we're interested in, and connect adjacent points by straight lines; when the points are close together, the length of each line segment will be close to the length along the parabola.

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a , 0 a , 0 and b , 0 b , 0 —in other words, a line segment located on the x -axis. Suppose we want to integrate over any curve in the plane, not just over a line segment on the x -axis. Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus.

Evaluate the line integral where c is the given curve

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space. Vector line integrals are integrals of a vector field over a curve in a plane or in space. We chop the curve into small pieces.

Xnxx com4k

Sometimes we have no choice but to use this parameterization. How could we quantify the rate at which the fluid is crossing C? Here, we calculate the mass of a wire using a scalar line integral and the work done by a force using a vector line integral. Did not receive OTP? Approximation 5. Whose line integral is larger and by how much? Concavity and inflection points 5. Explanation of solution. Let f x , y , z f x , y , z be a function with a domain that includes curve C. Therefore, the work done by F in moving the particle in the positive direction along C is defined as. The work done by the vector field depends on the direction in which the particle is moving. Q: Evaluate the line integral along the curve C. Derivatives of the exponential and logarithmic functions 8.

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course.

Properties of Functions 3 Rules for Finding Derivatives 1. When C has been given an orientation, C is called an oriented curve Figure 6. A line integral is also called the path integral or a curve integral or a curvilinear integral. A: Find the equation of line in parametric form. McGraw-Hill Education. In a later section we will investigate this idea in more detail. Here is the parameterization for this curve. Alternatively, if a curve on a map represents a road, we might want to know how far we need to drive to get to our destination. The reason for this is that the orientation of the curve flows against the direction of F. In this article, we are going to discuss the definition of the line integral, formulas, examples, and the application of line integrals in real life. Advanced Math. Volume 4. Geometry Read Explanation. Vector line integrals are integrals of a vector field over a curve in a plane or in space. However, there is no reason to restrict ourselves like that.