D dx of tan inverse x
The differentiation of tan inverse x is the process of finding the derivative of tan inverse x with respect to x. In this article, we will learn the concept of the derivative of arctan, its proof using implicit differentiation, the first principle of differentiation, and the derivative of tan inverse x with respect to cot inverse x along with some examples for a d dx of tan inverse x understanding. The derivative of tan inverse x can be calculated using different methods such as the first principle of derivatives and using implicit differentiation.
Before going to see what is the derivative of arctan, let us see some facts about arctan. Arctan or tan -1 is the inverse function of the tangent function. We use these facts to find the derivative of arctan x. We are going to prove it in two methods in the upcoming sections. The two methods are.
D dx of tan inverse x
We will also study several examples so that you fully understand the topic. Tangent is a trigonometric function, and if we take the inverse of this function, then it is called the inverse tangent function or arc tan function. The graph for the inverse tangent function is given as:. The graph for derivative of the tan inverse is given as:. For example, in this case, the formula for inverse tan x is the same as the inverse cot x, the only difference is the negative sign, so if you know the formula for inverse cot x, then by removing the negative sign you will get the formula for inverse tan x. The first principle method does not use other theorems. It uses the definition of derivative to solve any function. The general formula of the first principle method for a function f x is given as:. The expression will be equal to 1. According to implicit differentiation, if we are given an implicit function, then we take the derivative of the left-hand side and right side hand of the equation with respect to the independent variable.
United States. Kindergarten Worksheets. Already booked a tutor?
.
Derivative of tan inverse x refers to the process of finding the change in the inverse tangent function to the independent variable. The specific process of finding the derivative for inverse trigonometric functions is referred to as inverse trigonometric differentiation, and the derivative of tan -1 x is one of the key results in inverse trigonometric differentiation. In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. The derivative of a function is the rate of change of the function to any independent variable. The differentiation of an inverse trigonometric function is called a derivative of the inverse trigonometric function or inverse trig derivatives. Learn, Derivative. Among the inverse trig derivatives, the derivative of the tan -1 x is one of the derivatives. The derivative of tan -1 x is the rate of change to angle i. Learn, Inverse Trigonometric Derivative.
D dx of tan inverse x
The differentiation of the inverse tan function can be derived mathematically and it is used as a formula in differential calculus. So, let us learn how to derive the derivative rule for the inverse tan function. It is an indeterminate form and it clears that we cannot evaluate it mathematically by the direct substitution method. Now, comeback to the first step to find the derivative of inverse tangent function in another way. The limit of rational expression is almost similar to the limit rule of inverse tan function but the argument in the inverse tan function should be same in the denominator for using the formula. Now, use the product rule of limits to evaluate the limit of the product by the product of their limits. According to the limit rule of inverse trigonometric functions , the limit of quotient of inverse function by its argument is equal to one as its input approaches zero. A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects. Subtraction of the fractions with the Different denominators.
Condos for sale woodstock ga
To prove the derivative of tan inverse x using implicit differentiation , we will use the following trigonometric formulas and identities:. Search for:. About Us. Now we will evaluate the derivative of arctan using the first principle of differentiation. Learn Practice Download. Hence, we have calculated the derivative of tan inverse x using the first principle of derivatives. We have. Maths Questions. We will also study several examples so that you fully understand the topic. Derivative of Arctan Proof by First Principle 4. Privacy Policy. Online Tutors. Terms and Conditions. Breakdown tough concepts through simple visuals.
The differentiation of tan inverse x is the process of finding the derivative of tan inverse x with respect to x. In this article, we will learn the concept of the derivative of arctan, its proof using implicit differentiation, the first principle of differentiation, and the derivative of tan inverse x with respect to cot inverse x along with some examples for a better understanding. The derivative of tan inverse x can be calculated using different methods such as the first principle of derivatives and using implicit differentiation.
We are going to prove it in two methods in the upcoming sections. For example, in this case, the formula for inverse tan x is the same as the inverse cot x, the only difference is the negative sign, so if you know the formula for inverse cot x, then by removing the negative sign you will get the formula for inverse tan x. Learn Practice Download. Breakdown tough concepts through simple visuals. The general formula of the first principle method for a function f x is given as:. Before going to see what is the derivative of arctan, let us see some facts about arctan. It uses the definition of derivative to solve any function. Math worksheets and visual curriculum. Commercial Maths. The graph for the inverse tangent function is given as:. An easy way to memorize the derivative of tan inverse x is that it is the negative of the derivative of cot inverse x. Kindergarten Worksheets. Our Mission. United Kingdom.

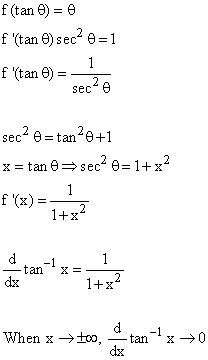
Instead of criticism write the variants.
What necessary phrase... super, excellent idea