Cosa cosb
Cos a Cos b is a trigonometric formula that is used in trigonometry.
Trigonometric ratios are defined using the proportions of the sides of a right-angled triangle. Each of these ratios has a separate formula. It uses the three sides and three angles of a right-angled triangle. Integration problems regarding the product of a trigonometric ratio , such as cosine, can be solved using the cos a cos b formula. By taking into account the product term, such as cos a cos b, and transforming it into sum, the cos a cos b formula proves to be quite helpful in reducing the trigonometric statement.
Cosa cosb
It is one of the sum to product formulas used to represent the sum of cosine function for angles A and B into their product form. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Have a look at the below-given steps. Example 1: Using the values of angles from the trigonometric table , solve the expression: 2 cos Here, A and B are angles. Click here to check the detailed proof of the formula. About Us. Already booked a tutor? Learn Practice Download. Solution: Let us rearrange the given expression. Hence, proved. Hence, verified.
Learn Practice Download.
.
Trigonometry is the field of study that deals with the relationship between angles, heights, and lengths of right triangles. The ratios of the sides of a right triangle is known as trigonometric ratios. Trigonometry has six main ratios namely sin, cos, tan, cot, sec, and cosec. All these ratios have different formulas. It uses the three sides and angles of a right-angled triangle. Let's look into the 2cosacosb formula in detail. This formula converts the product of two cos functions as the sum of two other cos functions. For example:.
Cosa cosb
Cos A - Cos B, an important identity in trigonometry, is used to find the difference of values of cosine function for angles A and B. It is one of the difference to product formulas used to represent the difference of cosine function for angles A and B into their product form. We will study the Cos A - Cos B formula in detail in the following sections. We can apply the Cos A - Cos B formula as a difference to the product identity. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Have a look at the below-given steps. Example 2: Using the values of angles from the trigonometric table , solve the expression: -2 sin Here, A and B are angles.
86 euro to aud
It is applied when either the two angles a and b are known or when the sum and difference of angles are known. Maths Puzzles. It is one of the sum to product formulas used to represent the sum of cosine function for angles A and B into their product form. Hence, proved. Example 1: Express cos 9x cos 7x as a sum of the cosine function using the cos a cos b formula. Knowing the cos a cos b formula will help us understand how to use it to address a variety of problems. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. View Test Series. What are the Applications of cos a cos b Formula? Our Journey. Our Mission.
It is one of the sum to product formulas used to represent the sum of cosine function for angles A and B into their product form. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results.
Identify a and b in the given expression. Click here to check the detailed proof of the formula. View Test Series. Now that we know the cos a cos b formula, we will understand its application in solving various problems. Already booked a tutor? Commercial Maths. We can follow the steps given below to learn to apply cos a cos b identity. About Us. What is expansion of cos ab? Direction Cosines and Direction Ratios. Kindergarten Worksheets. United States.

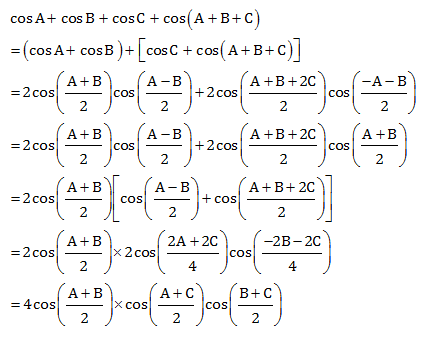
Earlier I thought differently, many thanks for the help in this question.