Cofunction identities examples
Cofunction Formulas are special relationships between certain trigonometric functions that help us understand complementary angles better. In this maths formula article, we will explore Cofunction Formulas and understand how they simplify trigonometric calculations. Cofunction Formulas, also known as Cofunction Identities, are a set of trigonometric identities cofunction identities examples establish relationships between the trigonometric functions of complementary angles, cofunction identities examples. In trigonometrythese identities play a significant role in simplifying calculations and problem-solving involving complementary angles.
Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Let us recall the meaning of complementary angles. Cofunction identities are trigonometric identities that show the relationship between trigonometric ratios pairwise sine and cosine, tangent and cotangent, secant and cosecant. We use the angle sum property of a triangle to derive the six cofunction identities. In this article, we will derive the cofunction identities and verify them using the sum and difference formulas of trigonometric functions. We will also solve various examples to understand the usage of these cofunction identities to solve various math problems involving trigonometric functions.
Cofunction identities examples
Welcome to Omni's cofunction calculator , where we'll study the cofunction identities and how to use them. In essence, in trigonometry, there are six functions that fully describe the relations between the angles and sides of a triangle. As such, they are connected to one another, so we often think of them as pairs: sin and cos, tan and cot, sec, and csc. Today we'll look into those relations and learn how to go from one map to its pair, i. Before we see what a cofunction is, we need to start with the basics. And in geometry, we can't go more basic than triangles: three sides, three vertices, three inside angles. In some sense, there can be no simpler polygon. We, however, are most interested in a particular type of triangle: right triangles you know, the ones that the Pythagorean theorem is all about. Moreover, we can observe some other dependencies that make the triangle look the way it does. After all, if we increase one of the acute angles, we can easily see that the opposite side will have to get longer too. This observation is, more or less, the idea behind trigonometry: to somehow relate a triangle's inside angles to its sides. We focused on that topic in our trigonometry calculator. We define trigonometric functions as ratios between a right triangle's sides. Below you can find a picture with the formulas for all six of them. Note how in the cofunction calculator, there's one identity for each of them.
We'll see the cofunction identities in detail in the next section. Two angles are said to be complementary if their sum is 90 degrees.
We already know the different trigonometric functions like sine, cosine, and tangent. But how can we determine the relationsip between them? The answer is cofunction identities. Now, why this is important? The cofunction identities establish the connection between the trigonometric functions. The soul of this connection is purely based on complementary angles. It is very important to understand the concept involving trigonometric cofunction identities to prepare yourself for the advanced topics.
In Section Not only did these identities help us compute the values of the circular functions for angles, they were also useful in simplifying expressions involving the circular functions. In this section, we introduce several collections of identities which have uses in this course and beyond. In light of the Quotient and Reciprocal Identities, Theorem Their true utility, however, lies not in computation, but in simplifying expressions involving the circular functions. We first prove the result for differences. The identity verified in Example These identities were first hinted at in Exercise 74 in Section Now that these identities have been established for cosine and sine, the remaining circular functions follow suit.
Cofunction identities examples
Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Let us recall the meaning of complementary angles. Cofunction identities are trigonometric identities that show the relationship between trigonometric ratios pairwise sine and cosine, tangent and cotangent, secant and cosecant.
Watch brooklyn 99 online season 2
Example 2. But don't sulk! Let us now verify the cofunction identities for sec, csc, and cot using reciprocal identities. We can write the cofunction identities in terms of radians and degrees as these are the two units of angle measurement. And with that, we declare the end of theory for today! Want to build a strong foundation in Math? Already booked a tutor? We know that tan and cotangent are cofunctions of each other. After all, if we increase one of the acute angles, we can easily see that the opposite side will have to get longer too. We already know that sin and cosine are cofunctions of each other.
We already know the different trigonometric functions like sine, cosine, and tangent. But how can we determine the relationsip between them? The answer is cofunction identities.
Similarly, secant and cosecant are cofunctions. This proof establishes the relationship between the cofunction formulas for sine and cosine ratios. Observe how each time the tool gives us a precise value i. Be sure to check it if you're in need! The cofunction identities give a relationship between trigonometric functions sine and cosine , tangent and cotangent, and secant and cosecant. Before we see what a cofunction is, we need to start with the basics. Although we won't give them here, we happily encourage you to look them up and enjoy some extra mathematical knowledge. Commercial Maths. It means we need to deal with complementary angles. Observe how we never mention how big the triangle is. We already know that sin and cosine are cofunctions of each other.

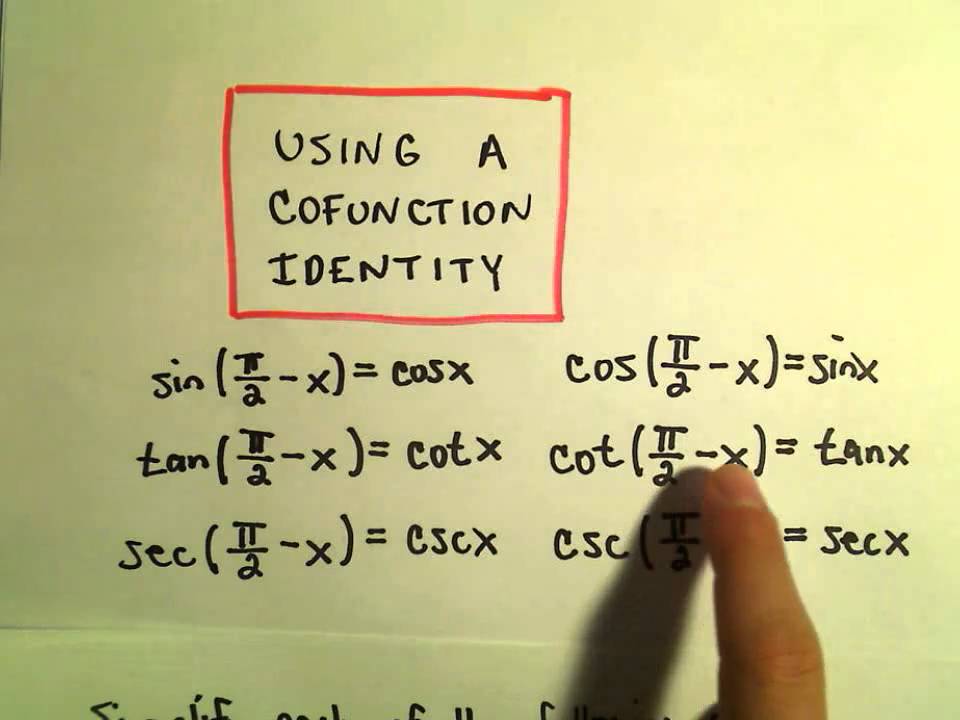
In it something is. Many thanks for the information, now I will know.
Should you tell you have deceived.