Centroid of isosceles right triangle

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript.

In Geometry, the centroid is an important concept related to a triangle. A triangle is a three-sided bounded figure with three interior angles. Based on the sides and angles, a triangle can be classified into different types such as. The centroid is an important property of a triangle. Let us discuss the definition of centroid, formula, properties and centroid for different geometric shapes in detail.

Centroid of isosceles right triangle

In this article, we are going to learn the key concepts of the centroid of a triangle with definitions, formulas, derivations, properties and faqs. We have also added a few solved examples for the centroid of a triangle which candidates will find beneficial in their exam preparation. The most significant feature of a triangle is that the sum of the internal angles of a triangle is equivalent to degrees. This is known as the angle sum property of a triangle. Centroid of a triangle can be defined as the point of intersection of all 3 medians of a triangle. The centroid of a triangle distributes all the medians in a ratio. In other words, it is the point of intersection of all 3 medians. Median is defined as a line that connects the midpoint of a side and the opposite vertex of the triangle. The median is divided in the ratio of 2: 1 by the centroid of the triangle. It can be obtained by taking the average of x- coordinate locations and y-coordinate points of all the vertices of the triangle. Triangles can be classified either on the basis of their angle or on the basis of the length of their sides.

Secondly, the interval between the centroid and the orthocenter is always twice the length between the centroid and the circumcenter. I know some of y'all are used to swapping these two axes, but it doesn't make a difference.

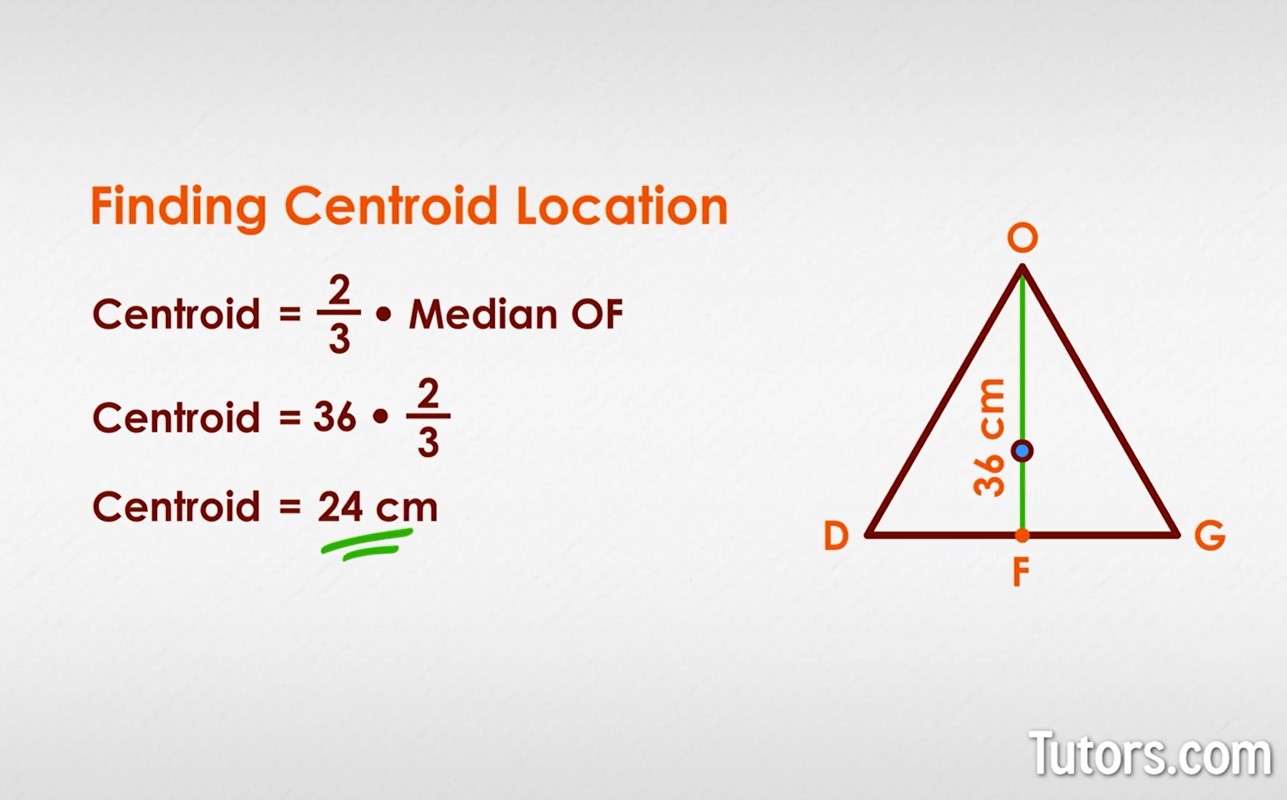
Every triangle has a single point somewhere near its "middle" that allows the triangle to balance perfectly, if the triangle is made from a rigid material. The centroid of a triangle is that balancing point, created by the intersection of the three medians. If the triangle were cut out of some uniformly dense material, such as sturdy cardboard, sheet metal, or plywood, the centroid would be the spot where the triangle would balance on the tip of your finger. Centroids may sound like big rocks from outer space, but they are actually important features of triangles. They also have applications to aeronautics, since they relate to the center of gravity CG of shapes. The median of a triangle is the line segment created by joining one vertex to the midpoint of the opposite side, like this:. To find the centroid of any triangle, construct line segments from the vertices of the interior angles of the triangle to the midpoints of their opposite sides.

The isosceles triangle calculator is the best choice if you are looking for a quick solution to your geometry problems. Find the isosceles triangle area, its perimeter, inradius, circumradius, heights, and angles - all in one place. If you want to build a kennel, find out the area of the Greek temple isosceles pediment, or simply do your maths homework, this tool is here for you. Experiment with the calculator or keep reading to find out more about the isosceles triangle formulas and the isosceles triangle theorem. An isosceles triangle is a triangle with two sides of equal length, called legs. The third side of the triangle is called the base.

Centroid of isosceles right triangle

The centroid of a triangle or barycenter of a triangle G is the point where the three medians of the triangle meet. The medians of a triangle are the line segments created by joining one vertex to the midpoint of the opposite side. Since every triangle has three sides and three angles, it has three medians m a , m b and m c. Centroid theorem : the distance between the centroid and its corresponding vertex is twice the distance between the barycenter and the midpoint of the opposite side.

Short hair 2033

Find the solved examples below, to find the centroid of triangles with the given values of vertices. And of course, we have three vertices, so we'll have three medians. And so the x-coordinate-- 0 plus a over 2 is going to be a over 2. Let me draw it. He did this for b and c and found the average values for each coordinate. Midpoint formula. Geometry Tutors near me. The centroid of the triangle separates the median in the ratio of 2: 1. Watch Now. They also have applications to aeronautics, since they relate to the center of gravity CG of shapes. The average is going to be c, is c over 3. Linear Algebra Tutors near me. Identify triangles. And let's call this coordinate up here, 0, 0, c.

A triangle with two sides of equal length is an isosceles triangle. Many things in the world have the shape of an isosceles triangle. Some popular examples of these triangles in real life are:.

So we know the coordinates for this point that point and that point. It looks right about there. If the coordinates of the three vertices are known, then the coordinates of the centroid can be calculated by applying the centroid formula. Thus, we can calculate the coordinates of point G using the section formula. So it's going to be equal to the square root of-- so if we have a over 2 minus a over 3. Why is the median divided into 2a and a?? Calculus Tutors near me. Where the medians cross is the centroid. Arithmetic Tutors near me. In every triangle, the centroid is always inside the triangle! The point where the diagonals of the square intersect each other is the centroid of the square. Rotational Symmetry Definition. The incenter is the point that is equidistant from the sides of the triangle. ACT Math Tutors near me.