3x-1
It probably came into being between the s and s, 3x-1.
It is also known as the Collatz problem or the hailstone problem. This leads to the sequence 3, 10, 5, 16, 4, 2, 1, 4, 2, 1, A sequence obtained by iterating the function from a given starting value is sometimes called "the trajectory" of that starting value. Obviously there can be no consecutive odd numbers in any trajectory, but there may certainly be consecutive even numbers, especially when the trajectory reaches a power of 4, in which the trajectory quickly plummets to 1 after passing through all the intervening powers of 2. Note that since the odd-indexed powers of 2 are congruent to 2 modulo 3, they are only reachable from halving a power of 4. See also reduced Collatz function.
3x-1
The Collatz conjecture [a] is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even , the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence. It is named after the mathematician Lothar Collatz , who introduced the idea in , two years after receiving his doctorate. Consider the following operation on an arbitrary positive integer :. Now form a sequence by performing this operation repeatedly, beginning with any positive integer, and taking the result at each step as the input at the next. The Collatz conjecture is: This process will eventually reach the number 1, regardless of which positive integer is chosen initially. If the conjecture is false, it can only be because there is some starting number which gives rise to a sequence that does not contain 1. Such a sequence would either enter a repeating cycle that excludes 1, or increase without bound.
Steiner proved that there is no 1-cycle other than the trivial 1; 2, 3x-1.
.
Please ensure that your password is at least 8 characters and contains each of the following:. Hope that helps! You'll be able to enter math problems once our session is over. New Messages. For a new problem, you will need to begin a new live expert session. You can contact support with any questions regarding your current subscription. I am only able to help with one math problem per session.
3x-1
A problem posed by L. Collatz in , also called the mapping, problem, Hasse's algorithm, Kakutani's problem, Syracuse algorithm, Syracuse problem, Thwaites conjecture, and Ulam's problem Lagarias Let be an integer. Then one form of Collatz problem asks if iterating. If negative numbers are included, there are four known cycles excluding the trivial 0 cycle : 4, 2, 1 , , , , , , , , and , , , , , , , , , , , , , , , , ,. The members of the sequence produced by the Collatz are sometimes known as hailstone numbers. Conway proved that the original Collatz problem has no nontrivial cycles of length. Lagarias showed that there are no nontrivial cycles with length. Conway also proved that Collatz-type problems can be formally undecidable.
Mario strikers iso
Home Journals Article. Lemma 5. The proof is based on the distribution of parity vectors and uses the central limit theorem. Therefore, proposition 6 is correct. This requires 2 k precomputation and storage to speed up the resulting calculation by a factor of k , a space—time tradeoff. Obviously a counterexample, if it exists, must not be a power of 2. Springer Verlag, New York, Pure hailstone numbers are those which do not occur in the trajectories of smaller numbers, while impure hailstone numbers are those which do occur in the trajectories of smaller numbers. What is not so obvious is whether every trajectory eventually reaches a power of 4. Part two includes proposition 4, proposition 5 and proposition 6, which prove that the equivalent conjecture is correct. She puts her studies on hold for a time to address some unresolved questions about her family's past. If, for some given b and k , the inequality. It probably came into being between the s and s.
Solve Practice Play.
Functiones et Approximatio, Commentarii Mathematici, 56, Article Talk. Therefore, one transformation of F 1 X is twice operation; one transformation of F 2 X is one time operation. Retrieved Discrete Impuls Systems. Number of steps for n to reach 1 are. The result of jumping ahead k is given by. JSTOR Conway proved that the problem. The Journal of Supercomputing. American Mathematical Society. Bibcode : AcAri. A are. Lamont Responding to this work, Quanta Magazine wrote that Tao "came away with one of the most significant results on the Collatz conjecture in decades".

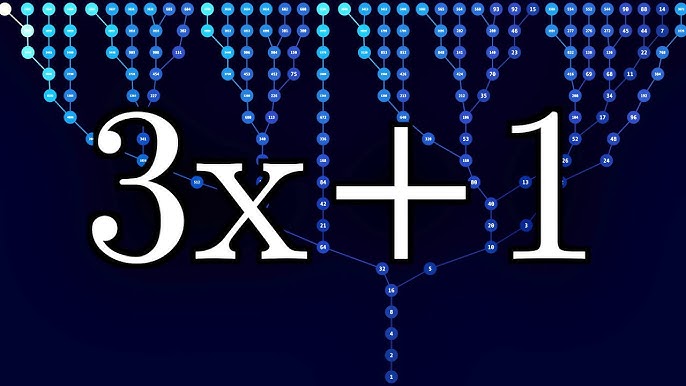
I am sorry, that has interfered... At me a similar situation. Let's discuss. Write here or in PM.